Figury płaskie, zadanie nr 1058

Autor	Zadanie / Rozwiązanie
dawiddab03 postów: 1	2019-05-23 17:31:03 Promień koła wpisanego w trapez równoramienny wynosi 2 a przekątna 5. Oblicz pole, wysokość i obwód tego trapezu? POMOCY NIE UMIEM DALEJ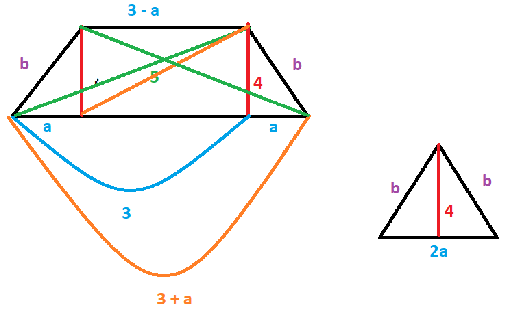

chiacynt postów: 749	2019-05-24 00:21:54 Poprawiamy rysunek, bo w taki trapez równoramienny nie wpiszesz okręgu ani koła. W jaki trapez można wpisać okrąg (koło)? Tylko w taki trapez w którym sumy długości - boków przeciwległych są równe . Wtedy $ h = 2r = 4.$ Przy Twoich oznaczeniach dłuższa podstawa trapezu jest równa $ a'= b' + a. $ Krótsza podstawa trapezu z Twierdzenia Pitagorasa wynosi $ b'^2 + 4^2 + 5^2 $ $ b' = 3.$ Długość dłuższej podstawy jest więc równa $ a' = 3 + a $ Długość najdłuższego ramienia trapezu $ b $ obliczamy też z Twierdzenia Pitagorasa: $ b^2 = a^2 + 4^2 \ \ (1) $ Dodajemy do równania $ (1) $ jeszcze jedno równanie, wynikające z możliwości wpisania okręgu (koła) w czworokąt, jakim jest trapez prostokątny równoramienny: $a' + b' = b + h, $ czyli $ a + 3 + 3 = b + 4 $ (sumy długości przeciwległych boków trapezu muszą być równe). Stąd $ a = b - 2 \ \ (2) $ Proszę rozwiązać układ równań $ (1), (2), $ wyznaczając długości odcinków $ a, b. $ $ a = 3, \ \ b = 5.$ Następnie obliczamy obwód i pole tego trapezu. $ Obwód = 6+4+3+5 = 18 ,$ $ Pole = \frac{6+3}{2}\cdot 4 = 18. $ Wiadomość była modyfikowana 2019-05-24 07:17:05 przez chiacynt

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj