Graniastosłupy, zadanie nr 780

Autor	Zadanie / Rozwiązanie
pk09890 postów: 9	2015-03-12 19:40:18 2 graniastoslupy prawidlowe mają tę samą wysokość. Podstawą pierwszego graniastoslupa jest kwadrat wpisany w okrąg o promieniu 1. Podstawa drugiego graniastoslupa jest trojkatem rownobocznym opisanym na okręgu o promieniu 1. Pole powierzchni całkowitej drugiego graniastoslupa jest dwa razy większe niż pole powierzchni cqlkowitej bryły pierwszej. Oblicz jaka wysokość mają tę graniatoslupy.

tumor postów: 8070	2015-03-13 17:59:50 jeśli a jest bokiem kwadratu, b jest bokiem trójkąta, to $a=\sqrt{2}$ $\frac{1}{3}\frac{b\sqrt{3}}{2}=1$ stąd $b=2\sqrt{3}$ Pole pierwszego graniastosłupa $P_a=2a^2+4ah$ Pole drugiego $P_b=2\frac{b^2\sqrt{3}}{4}+3bh$ No i mamy $P_b=2P_a$ Wstawiamy co znamy, wyliczamy h.

pk09890 postów: 9	2015-03-13 19:02:42 Tu rodzi się problem, ponieważ tam pojawiają się dość skomplikowane równania. Mogę prosić o dalsze rozwiązanie zadania?

klej postów: 1	2016-01-31 00:06:10 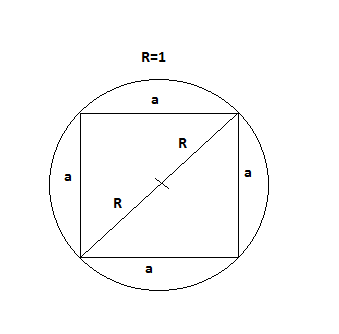$$ $a\times\sqrt{2}=2R$ $a\times\sqrt{2}=2$ $a=2\div\sqrt{2}=\sqrt{2}$ $pole_{podstawy1}=a^{2}$ $pole_{powierzchni całkowitej1}=2a^{2}+ 4ah = 4+ 4\sqrt{2} h$ 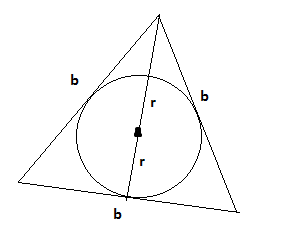$r=1$ $r=\frac{1}{3}\times h$$\iff h=3$ $h=\frac{b \sqrt{3}}{2}$ $3=\frac{b \sqrt{3}}{2}$$\iff$$b=2 \sqrt{3}$ $Pole podstawy2 = \frac{b^{2} \sqrt{3}}{4}$ $Pole podstawy2 = \frac{(2\sqrt{3)}^{2}\times\sqrt{3}}{4}$$=3\sqrt{3}$ $Polepowierzchnicałkowitej = 2\times 3\sqrt{3}+ 3\times bh=6\sqrt{3}+3\times 2\sqrt{3} h=6\sqrt{3}+ 6\sqrt{3} h$ Pole powierchni całkowitej drugiego graniastosłupa jest 2 razy większe niż pole pierwszego. $2\times(4+4\sqrt{2} h)= 6\sqrt{3}+6\sqrt{3} h$ $8+8\sqrt{2} h = 6\sqrt{3} + 6\sqrt{3} h$ $8\sqrt{2} h - 6\sqrt{3} h = 6\sqrt{3} - 8$ $h\times(8\sqrt{2} - 6\sqrt{3}) = 6\sqrt{3}- 8$ $h = \frac{6\sqrt{3} - 8}{8\sqrt{2} - 6\sqrt{3}}$ Mam nadzieję, że rozwiązanie jest zrozumiałe i poprawne, choć wynik jest dziwny.

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj