Matura z matematyki - poziom podstawowy
Zadania zamknięte
Zadanie 1.
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności |x + 7| > 5
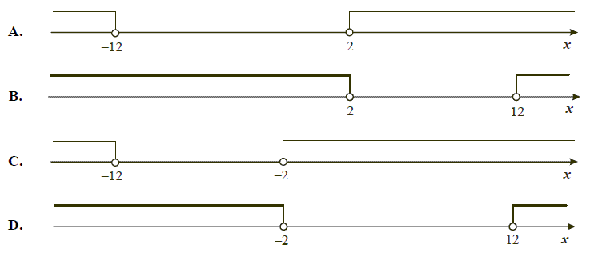
Rozwiązanie
|x + 7| > 5
x + 7 > 5 i x + 7 < -5
x > -2 i x < -12
Rozwiązaniem nierówności jest przedział liczbowy (-∞, -12)∩(-2, ∞)
Prawidłowa odpowiedĽ: C.
Zadanie 2.
Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
A. 163,80 zł B. 180 zł C. 294 zł D. 420 zł
Rozwiązanie
Niech x oznacza cenę spodni przed obniżką.
30% z x - obniżka
x - 0,3x = 126
0,7x = 126 / : 0,7
x = 180
Spodnie przed obniżką kosztowały 180 zł.
Prawidłowa odpowiedĽ: B.
Zadanie 3.
A. 1 B. 4 C. 9 D. 36
Rozwiązanie
Dowolna liczba podniesiona do potęgi zerowej równa się 1.
Prawidłowa odpowiedĽ: A.
Zadanie 4.
Liczba log48 + log42 jest równa
A. 1 B. 2 C. log46 D. log410
Rozwiązanie
Korzystamy z prawa działań na logarytmach
log48 + log42 = log4(8 · 2) = log416 = 2.
Prawidłowa odpowiedĽ: B.
Zadanie 5.
Dane są wielomiany W(x) = -2x3 + 5x2 - 3 oraz P(x) = 2x3 +12x . Wielomian W(x) + P(x) jest równy
A. 5x2 + 12x - 3
B. 4x3 + 5x2 + 12x - 3
C. 4x6 + 5x2 + 12x - 3
D. 4x3 + 12x2 - 3
Rozwiązanie
Prawidłowa odpowiedĽ: A.
Zadanie 6.
Rozwiązaniem równania jest
A. 1 B. C. D. 7
Rozwiązanie
Obliczamy dziedzinę równania:
7x + 1 ≠ 0
7x ≠ 1
x ≠
5(3x - 1) = 2(7x + 1)
15x - 5 = 14x + 2
x = 7
Prawidłowa odpowiedĽ: D.
Zadanie 7.
Do zbioru rozwiązań nierówności (x - 2)(x + 3) < 0 należy liczba
A. 9 B. 7 C. 4 D. 1
Rozwiązanie
(x - 2)(x + 3) < 0
Najłatwiej i najszybciej zadanie rozwiązać można podstawiając cztery podane wartości do nierówności.
(9 - 2)(9 + 3) < 0 ⇒ 84 < 0, fałsz
(7 - 2)(7 + 3) < 0 ⇒ 50 < 0, fałsz
(4 - 2)(4 + 3) < 0 ⇒ 24 < 0, fałsz
(1 - 2)(1 + 3) < 0 ⇒ -4 < 0, prawda
Prawidłowa odpowiedĽ: D.
Zadanie 8.
Wykresem funkcji kwadratowej f(x) = -3x2 + 3 jest parabola o wierzchołku w punkcie
A. (3,0) B. (0,3) C. (-3,0) D. (0,-3)
Rozwiązanie
f(x) = -3x2 + 3
a = -3, b = 3, c = 0;
Wykresem funkcji kwadratowej jest parabola o wierzchołku
Delta:
Wierzchołek paraboli:
Prawidłowa odpowiedĽ: B.
Zadanie 9.
Prosta o równaniu y = -2x + (3m + 3) przecina w układzie współrzędnych oś OY w punkcie (0, 2). Wtedy
A.
B.
C.
D.
Rozwiązanie
Prosta o równaniu ogólnym y = ax+ b przecina oś OY w punkcie (0, b).
Zachodzi więc 2 = 3m + 3
3m = -1
Prawidłowa odpowiedĽ: B.
Zadanie 10.
Na rysunku jest przedstawiony wykres funkcji y = f(x).
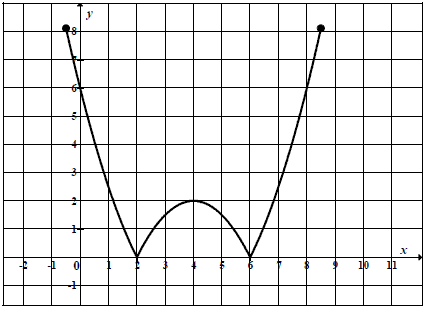
Które równanie ma dokładnie trzy rozwiązania?
A. f(x) = 0 B. f(x) = 1 C. f(x) = 2 D. f(x) = 3
Rozwiązanie
Korzystając z rysunku odczytujemy
Dla f(x) = 0 funkcja ma 2 rozwiązania
Dla f(x) = 1 funkcja ma 4 rozwiązania
Dla f(x) = 2 funkcja ma 3 rozwiązania
Dla f(x) = 3 funkcja ma 2 rozwiązania
Prawidłowa odpowiedĽ: C.
Zadanie 11.
W ciągu arytmetycznym (an) dane są: a3 = 13 i a5 = 39. Wtedy wyraz a1 jest równy
A. 13 B. 0 C. -13 D. -26
Rozwiązanie
Wyraz a4 jest średnią arytmetyczną wyrazów a3 i a5.
a4 =
Różnica ciągu arytmetycznego wynosi r = 26 - 13 = 13
Wyraz a3 = 13, więc wyraz a1 = a3 - 2 · r
= 13 - 2 · 13 = -13
Prawidłowa odpowiedĽ: C.
Zadanie 12.
W ciągu geometrycznym (an) dane są: a1 = 3 i a4 = 24. Iloraz tego ciągu jest równy
A. 8 B. 2 C. D.
Rozwiązanie
Iloraz ciągu geometrycznego równy jest .
Korzystamy ze wzoru na n-ty wyraz ciągu geometrycznego:
an = a1 · qn-1 dla n ≥ 2.
Obliczamy iloraz q z wyrazu czwartego
a4 = a1 · q3
24 = 3 · q3
q3 = 8
Prawidłowa odpowiedĽ: B.
Zadanie 13.
Liczba przekątnych siedmiokąta foremnego jest równa
A. 7 B. 14 C. 21 D. 28
Rozwiązanie
Liczba przekątnych w n-kącie równa jest
= 14
Prawidłowa odpowiedĽ: B.
Zadanie 14.
Kąt α jest ostry i . Wartość wyrażenia jest równa
A.
B.
C.
D.
Rozwiązanie
Korzystamy z jedynki trygonometrycznej:
, z której obliczamy
Obliczamy teraz wartość wyrażnia
Prawidłowa odpowiedĽ: A.
Zadanie 15.
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa
A. B. C. 8 D. 4
Rozwiązanie
Przekątna kwadratu jest dwa razy dłuższa od promienia okręgu opisanego na nim.
Przekątna kwadratu równa jest d = 8.
Niech a oznacza długość boku kwadratu
Korzystamy bezpośrednio ze wzoru na przekątną kwadratu lub
z twierdzenia Pitagorasa:
Prawidłowa odpowiedĽ: A.
Zadanie 16.
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę
ma długość
A. 3 B. 4 C. D.
Rozwiązanie
Rysunek do zadania:
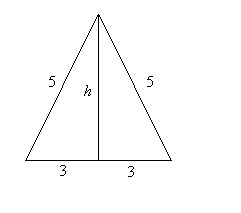
Wysokość tójkąta liczymy z twierdzenia Pitagorasa:
W naszym wypadku mamy:
Uwaga: spoglądając na rysunek warto zauważyć, że mamy do czynienia z trójkątem egipskim, często obecnym trójkątem pitagorejskim (3, 4, 5).
Prawidłowa odpowiedĽ: B.
Zadanie 17.
Odcinki AB i DE są równoległe. Długości odcinków CD, DE i AB są
odpowiednio równe 1, 3 i 9. Długość odcinka AD jest równa
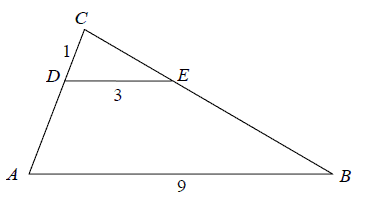
A. 2 B. 3 C. 5 D. 6
Rozwiązanie
Korzystamy z tw. Talesa
|AD| = 2
Prawidłowa odpowiedĽ: A.
Zadanie 18.
Punkty A, B, C leżące na okręgu o środku S są wierzchołkami trójkąta równobocznego
Miara zaznaczonego na rysunku kąta środkowego ASB jest równa
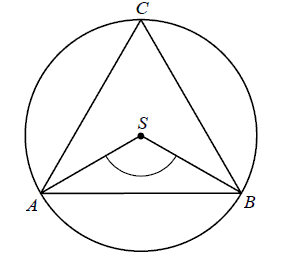
A. 120° B. 90° C. 60° D. 30°
Rozwiązanie
Kąt przy wierzchłku c ma miarę 60°.
Miara kąta środkowego jest dwa razy większa od miary kąta wpisanego opartego na tym samym łuku co kąt środkowy.
Miara kąta ASB jest równa 120°
Prawidłowa odpowiedĽ: A.
Zadanie 19.
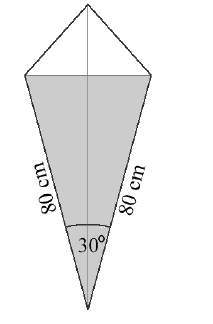
Latawiec ma wymiary podane na rysunku. Powierzchnia zacieniowanego trójkąta jest równa
A. 3200 cm2
B. 6400 cm2
C. 1600 cm2
D. 800 cm2
Rozwiązanie
Korzystamy ze wzoru:
cm2
Prawidłowa odpowiedĽ: C.
Zadanie 20.
Współczynnik kierunkowy prostej równoległej do prostej o równaniu y = -3x + 5 jest równy:
A.
B. -3
C.
D. 3
Rozwiązanie
Proste w układzie współrzędnych są równoległe wtedy i tylko wtedy, gdy współczynniki
kierunkowe tych prostych są równe.
Prawidłowa odpowiedĽ: B.
Zadanie 21.
Wskaż równanie okręgu o promieniu 6.
A. x2 + y2 = 3 B. x2 + y2 = 6 C. x2 + y2 = 12 D. x2 + y2 = 36
Rozwiązanie
Równanie okręgu o środku w punkcie (a, b) i promieniu r:
(x - a)2 + (y - b)2 = r2
62 = 36
Prawidłowa odpowiedĽ: D.
Zadanie 22.
Punkty A = (-5, 2) i B = (3, -2) są wierzchołkami trójkąta równobocznego ABC.
Obwód tego trójkąta jest równy
A. 30
B.
C.
D. 36
Rozwiązanie
Jeżeli dane są punkty A(xa; ya) i
B(xb; yb) na płaszczyĽnie, to długość odcinka |AB| obliczamy ze wzoru
Obwód trójkąta równy jest
Prawidłowa odpowiedĽ: C.
Zadanie 23.
Pole powierzchni całkowitej prostopadłościanu o wymiarach 5×3×4 jest równe
A. 94 B. 60 C. 47 D. 20
Rozwiązanie
Prawidłowa odpowiedĽ: A.
Zadanie 24.
Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A. 11 B. 18 C. 27 D. 34
Rozwiązanie
Jeśli przez w oznaczymy liczbę wierzchołków ostrosłupa to liczba krawędzi równa się 2(w - 1)
2(18 - 1) = 34
Prawidłowa odpowiedĽ: D.
Zadanie 25.
Średnia arytmetyczna dziesięciu liczb x, 3, 1, 4, 1, 5, 1, 4, 1, 5 jest równa 3. Wtedy
A. x = 2 B. x = 3 C. x = 4 D. x = 5
Rozwiązanie
Mnożymy obustronnie równanie przez 10 i otrzymujemy
x + 3 + 1 + 4 + 1 + 5 + 1 + 4 + 1 + 5 = 30
x = 30 - 25
x = 5
Prawidłowa odpowiedĽ: D.
Zadania otwarte
Zadanie 26.
Rozwiąż nierówność x2 - x - 2 ≤ 0.
Rozwiązanie
x2 - x - 2 ≤ 0
Współczynniki liczbowe:
Delta:
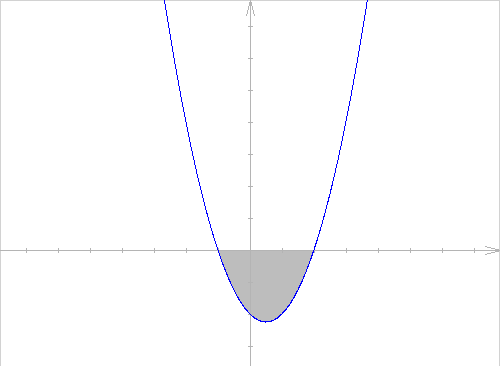
Rozwiązaniem nierówności są x ∈ <-1, 2>
Zadanie 27.
Rozwiąż równanie x3 - 7x2 - 4x + 28 = 0 .
Rozwiązanie
Równanie grupujemy oraz korzystając ze wzorów skróconego mnożenia przekształcamy.
Rozwiązaniem równania są
,
,
Zadanie 28.
Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku
(w obu trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że |AD| = |BE|.
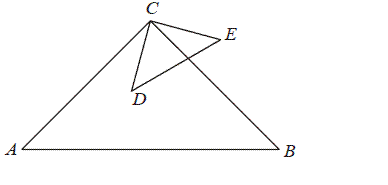
Rozwiązanie
Długości boków AC i CB są równe, oraz boki CD i CE są także tej samej długości.
Miary kątów ACD i BCE są jednakowe.
Jeżeli dwa boki i kąt między nimi zawarty jednego trójkąta są odpowiednio równe dwóm bokom i kątowi między
nimi zawartemu drugiego trójkąta, to trójkąty są przystające.
Zatem trójkąty ACD i BCE są przystające, więc |AD| = |BE|.
Zadanie 29.
Kąt α jest ostry i . Oblicz cosα.
Rozwiązanie
Kąt α, więc cosα > 0.
Podnosimy obie strony do kwadratu i otrzymujemy
Podstawiamy do jedynki trygonometrycznej:
Zadanie 30.
Wykaż, że jeśli a > 0, to
Rozwiązanie
Mnożymy obie strony nierówności przez 2(a + 1). Znak nierówności nie zmieni się, ponieważ a > 0.
Nierówność ta jest zawsze prawdziwa w zbiorze liczb rzeczywistych,
więc dla a > 0 nierówność jest także prawdziwa, co należało wykazać.
Zadanie 31.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny.
Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Rozwiązanie
Rysunek do zadania
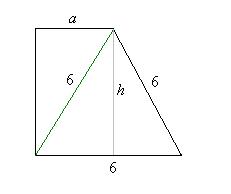
Długość podstawy dolnej i nie prostopadłego ramienia trapezu wynosi 6.
Wysokość h trójkąta i zarazem trapezu ma długość
Długość boku a jest równa połowie podstawy trójkąta równobocznego i wynosi 3.
Możemy także policzyć z twierdzenia Pitagorasa długość górnej podstawy trapezu a zakładając, że a > 0
Obwód trapezu równy jest .
Zadanie 32.
Podstawą ostrosłupa ABCD jest trójkąt ABC. KrawędĽ AD jest wysokością ostrosłupa (zobacz rysunek).
Oblicz objętość ostrosłupa ABCD, jeśli wiadomo, że |AD| = 12, |BC| = 6,
|BD| = |CD| = 13.
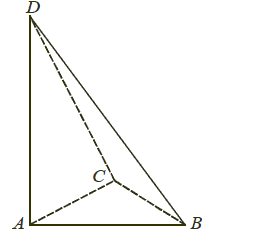
Rozwiązanie
|BD| = |CD| = 13
H = |AD| = 12
|BC| = 6
Do obliczenia objętości potrzeba policzyć pole podstawy ostrosłupa.
Znamy długości boków trójkąta CBD, w którym możemy policzyć wysokość h1
z tw. Pitagorasa. Przy obliczaniu zakładamy, ze wszystkie wielkości są większe od zera.
Znając wysokość trójkąta CBD i wysokość ostrosłuba AD możemy policzyć wysokość trójkąta ABC również z tw. Pitagorasa.
Objętość ostrosłupa równa jest
.
Zadanie 33.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry.
Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że w pierwszym rzucie
otrzymamy parzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 12.
Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Rozwiązanie
Wszystkich możliwych wyników przy dwukrotnym rzucie kostą sześcienną jest 62 = 36.
A - zdarzenie polegające na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn
liczb oczek w obu rzutach będzie podzielny przez 12.
Wypisujemy zbiór zdarzeń sprzyjających:
Moc zbioru A wynosi 6 (jest sześć sprzyjających zdarzeń).
.
Zadanie 34.
W dwóch hotelach wybudowano prostokątne baseny. Basen w pierwszym hotelu
ma powierzchnię 240 m2. Basen w drugim hotelu ma powierzchnię 350 m2 oraz jest o 5 m
dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny
w obu hotelach. Podaj wszystkie możliwe odpowiedzi.
Rozwiązanie
.
Drugie równanie ma postać .
W miejsce xy wstawiamy wartość 240 i otrzymujemy 5x + 2y = 100.
Z pierwszego równania wyznaczamy i wstawiamy do drugiego równania.
Rozwiązujemy równanie kwadratowe.
Współczynniki liczbowe:
Delta:
Dla
dla .
Wymiary basenów w hotelach mogą mieć wymiary 8 m × 30 m i 10 m × 35 m lub 12 m × 20 m i 14 m × 25 m.