Zbiór zadań, (zadania różne)
Zadanie 175
Dla ilu liczb naturalnych n zbiór wszystkich wierzchołków n-kąta foremnego można podzielić na takie dwa podzbiory, aby w żadnym z tych podzbiorów nie znajdowały się trzy punkty, które są wierzchołkami trójkąta równoramiennego?
Rozwiązanie
Rozpatrzmy przypadki:
n = 3 i n = 4 spełnia warunki zadania co łatwo wykazać.
n = 5:
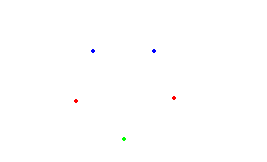
Liczba wierzchołków jest nieparzysta, więc do jednego z podzbiorów będą należały dwa kolejne wierzchołki. Niech to będą wierzchołki koloru niebieskiego. Jeśli do drugiego podzbioru będą należały wierzchołki koloru czerwonego, to pozostały (zielony)wierzchołek nie może należeć ani do zbioru pierwszego, ani do drugiego, gdyż z trzech wierzchołków powstanie trójkąt równoramienny.
Liczba 5 nie spełnia warunków zadania.
n = 6:
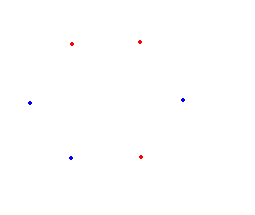
Rysunek powyżej jest przykładem takiego wyboru punktów (podzbiorów), w których dowolne wierzchołki nie utworzą trójkąta równoramiennego.
Liczba 6 spełnia warunki zadania.
n = 7:
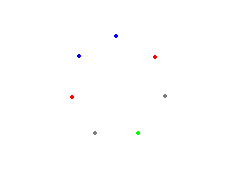
Niech do zbioru pierwszego należą dwa kolejne wierzchołki (kolor niebieski). Sąsiadujące z nimi wierzchołki będą należały do podzbioru drugiego (kolor czerwony). Wierzchołek oznaczony kolorem zielonym nie może należeć ani do zbioru pierwszego, ani do drugiego. Liczba 7 nie spełnia warunków zadania.
n = 8:
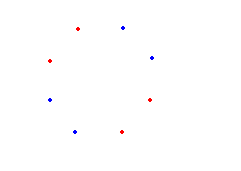
Rysunek powyżej jest przykładem takiego wyboru punktów (podzbiorów), w których dowolne trzy wierzchołki tego samego koloru nie utworzą trójkąta równoramiennego.
Liczba 8 spełnia warunki zadania.
Dla n większych lub równych od 9 nie istnieją takie podzbiory, które spełniałyby warunki zadania. Jeśli ponumerujemy kolejno wierzchołki n-kąta foremnego: 1, 2, ,3, 4, ..., n, gdzie n > 8, to zakładając, że takie podzbiory istnieją mamy: Niech wierzchołki 2 i 3 należą do podzbioru pierwszego, wówczas wierzchołki 1 i 4 muszą należeć do podzbioru drugiego. Stąd wniosek że wierzchołek 7 musi należeć do podzbioru pierwszego, a wierzchołek 5 do podzbioru drugiego. Dalej wierzchołek 6 należy do pierwszego podzbioru, zaś wierzchołek 8 do podzbioru drugiego. Stąd wierzchołek 9 nie może należeć ani do podzbioru pierwszego, ani do drugiego, co jest sprzeczne z założeniem.
Tylko dla n = 3, 4, 6, 8 spełnione są warunki zadania.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>