logowanie

Sprawdzian szóstoklasisty 2010

Arkusz sprawdzianu przeprowadzonego 8 kwietnia 2010 roku.
Arkusz egzaminacyjny dla uczniów bez dysfunkcji i uczniów z dysleksją rozwojową (PDF)

Rozwiązania i komentarze do niektórych zadań.

Zadanie 8. Na igrzyskach w Londynie dystans maratonu zwiększono o 2,195 km. Ile to metrów?
A. 21950 m
B. 2195 m
C. 219,5 m
D. 2,195 m

Rozwiązanie:
1 km = 1000 m
Stąd 2,195 = 2195 m

Zadanie 9. Uczestnicy biegu startowali co dwie minuty. Pierwszy zawodnik wystartował o godzinie 9.05, a ostatni o 9.37. Ilu zawodników wzięło udział w biegu?
A. 15 B. 17 C. 32 D. 42
Rozwiązanie:
37 minut - 5 min = 32 minuty. Taki była róznica miedzy pierwszym a ostatnim startującym.
32 : 2 + 1 = 17.

Zadanie 14. Która z figur ma kształt trójkąta prostokątnego równoramiennego?

Rozwiązanie:
Za pomocą ekierki sprawdzić kąt prosty w trójkątach. Za pomocą linijki sprawdzić długość boków trójkąta i określić który z nich to trójkąt prostokątny równoramienny.
Komentarz: Co bystrzejszy uczeń zapewne bez przyrządów z łatwością ocenił, który z trójkątów jest rozwiązaniem zadania.

Zadanie 15. Boisko ma kształt prostokąta o wymiarach 45 m i 90 m. Ile metrów kwadratowych ma to boisko?
A. 4050 B. 2025 C. 270 D. 135
Rozwiązanie:
Pole prostokąta: P = 45 · 90 = 4050 m²

Zadanie 16. Na planie prostokątnego boiska zamalowano część powierzchni, na której zostanie wymieniona nawierzchnia

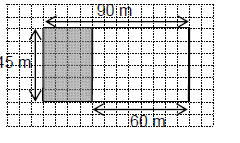
Na jakiej części boiska zostanie wymieniona nawierzchnia?
A. $\frac{1}{2}$ B. $\frac{2}{3}$ C. $\frac{1}{3}$ D. $\frac{3}{4}$
Rozwiązanie:
Powierzchnia boiska wynosi 45 · 90 = 4050 m²
Zamalowana część ma powierzchnię 30 · 45 = 1350 m²
Zatem jest to $\frac{1350}{4050}=\frac{1}{3}$ powierzchni boiska.
Komentarz: oczywiście wystarczy spojrzeć na rysunek aby dostrzec, że tylko odpowiedĽ C jest prawidłowa

Zadanie 17. Zawodnicy jednej drużyny wzięli ze skrzynki 5 butelek wody mineralnej, a zawodnicy drugiej drużyny dwa razy więcej. Ile butelek wody zostało w skrzynce?
Do rozwiązania tego zadania brakuje informacji, ile butelek wody
A. może pomieścić skrzynka.
B. wzięli zawodnicy drugiej drużyny.
C. wzięli razem zawodnicy jednej i drugiej drużyny.
D. było w skrzynce, zanim zaczęli je brać zawodnicy.
Rozwiązanie:
Ile butelek wody zostało w skrzynce?
Na to pytanie można odpowiedzieć wówczas, gdy będziemy wiedzieli ile było butelek w skrzynce zanim zaczęli je brać zawodnicy.

Zadanie 21. Maksymalną długość nart dla skoczka oblicza się, mnożąc wzrost zawodnika przez 1,46. Oblicz maksymalną długość nart dla zawodnika o wzroście 1,5 m. Wynik wyraĽ w centymetrach.
Rozwiązanie:
1,5 m · 1,46 = 2,19 m
2,19 m = 219 cm
OdpowiedĽ: Dla zawodnika mierzącego 1,5 m narty mogą mieć maksymalnie 219 cm długości.

Zadanie 22. Podczas meczu koszykówki Paweł trafił do kosza 5 razy, Leszek miał 2 razy więcej trafień niż Paweł, a Zbyszek o 3 mniej niż Paweł i Leszek razem. Ile razy trafił do kosza Leszek, a ile Zbyszek?
Rozwiązanie:
Paweł: 5 trafień
Leszek: 2 · 5 = 10 trafień
Zbyszek: (5 + 10) - 3 = 12 trafień
OdpowiedĽ: Leszek trafił do kosza 10 razy, a Zbyszek 12 razy.

Zadanie 23. Na planie w skali 1 : 50 000 trasa wyścigu ma długość 16,4 cm. Ile kilometrów mają do pokonania uczestnicy wyścigu?
Rozwiązanie:
1 cm na mapie odpowiada 50 000 cm w rzeczywistości, czyli 500 m lub 0,5 km
16,4 · 0,5 km = 8,2 km
OdpowiedĽ: Uczestnicy mają do pokonania 8,2 km.

Zadanie 24. Przy zakupie roweru na raty pierwsza wpłata wyniosła 176 zł. Pozostała do zapłaty kwota została rozłożona na 12 rat po 52 zł. Za ten sam rower kupiony za gotówkę zapłacono tylko $\frac{4}{5}$ ceny roweru kupionego na raty. Ile złotych kosztował rower kupiony za gotówkę?
Rozwiązanie:
Roweru kupiony na raty kosztuje: 176 zł + 12 · 52 zł = 800 zł
Rower kupiony za gotówkę: $\frac{4}{5}·800=640$ zł
OdpowiedĽ: Rower kupiony za gotówkę kosztował 640 zł.

© 2023 math.edu.pl      kontakt