Wartość bezwzględna

Wartością bezwzględną (modułem) liczby $x$ nazywamy liczbę spełniającą warunek:
$|x| = \left\{\begin{matrix} x \text{dla} x \geq 0 \\ - x \text{dla} x \lt 0 \end{matrix}\right. $
Wartość bezwzględną liczby $x$ zapisujemy symbolicznie $|x|$.

Wartością bezwzględną liczby nieujemnej jest ta sama liczba.
Wartością bezwzględną liczby ujemnej jest przeciwna do niej liczba dodatnia.

Uogólnieniem pojęcia wartości bezwzględnej na liczby zespolone jest moduł określany wzorem
$|x + y \cdot i| = \sqrt{x^2 + y^2}$, dla $x, y \in R$.

Interpretacja geometryczna wartości bezwzględnej

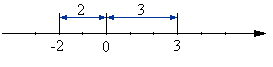
Wartość bezwzględna to odległość liczby od zera na osi liczbowej.
$|-2| = 2$
$|3| = 3$

Własności wartości bezwzględnej

$|x| \ge 0$
$|x| = |-x|$
$-|x| \le x \le |x|$
$|x| = \sqrt{x^2}$

$|a + b| \le |a| + |b|$
$|a - b| \le |a| + |b|$
$|a \cdot b| \le |a| \cdot |b|$
$\frac{|a|}{|b|} = |\frac{a}{b}|$, dla $b \neq 0$

Przykłady

|-15| = 15
|0| = 0
|25| = 25

W przypadku sumy (różnicy) składającej się ze składników niewymiernych musimy sprawdzić, czy suma (różnica) jest dodatnia czy ujemna, a następnie skorzystać z definicji.
$|3 - \sqrt{3}| = |\sqrt{9} - \sqrt{3}| > 0 \Rightarrow |3 - \sqrt{3}| = 3 - \sqrt{3}$
$|2 - \sqrt{5}| = |\sqrt{4} - \sqrt{5}| < 0 \Rightarrow |2 - \sqrt{5}| = - (2 - \sqrt{5}) = - 2 + \sqrt{5}$
$|2\sqrt{3} - 3\sqrt{2}| = |\sqrt{12} - \sqrt{18}| < 0 \Rightarrow |2\sqrt{3} - 3\sqrt{2}| = - (2\sqrt{3} - 3\sqrt{2}) = - 2\sqrt{3} + 3\sqrt{2}$

Równania z wartością bezwzględną