Funkcja liniowa

Funkcję $f$ określoną wzorem $f(x) = ax + b$ dla $x \in R$, gdzie $a, b \in R$ nazywamy funkcją liniową. Liczbę $a$ nazywamy współczynnikiem kierunkowym, liczbę b nazywamy wyrazem wolnym.

Wykres funkcji liniowej
Wykresem funkcji liniowej $f$ określonej wzorem $f(x) = ax + b$ dla $x \in R$ jest linia prosta nachylona do osi $OX$ pod kątem $\alpha$, gdzie $a = tg\alpha$ i przecinająca oś $OY$ w punkcie $(0, b)$.

Miejsce zerowe funkcji liniowej
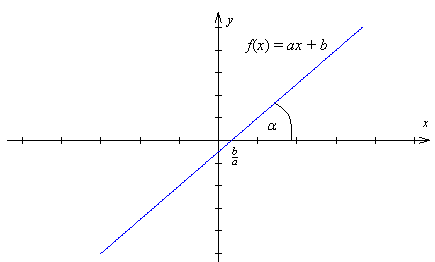
Miejsce zerowe funkcji to argument, dla którego dana funkcja przyjmuje wartość $0$. Interpretacją geometryczną miejsca zerowego jest odcięta punktu, w którym wykres funkcji przecina albo styka się z osią $OX$ w prostokątnym układzie współrzędnych.
Jeżeli funkcja $f(x) = ax + b$ nie jest funkcją stałą, to posiada ona dokładnie jedno miejsce zerowe określone wzorem $-\frac{b}{a}$,
Jeżeli funkcja $f$ jest funkcją stałą, to albo nie posiada miejsc zerowych (dla $b \neq 0$), albo wszystkie jej argumenty są miejscami zerowymi (dla $b = 0$).

Monotoniczność funkcji liniowej
Monotoniczność funkcji liniowej zależy od współczynnika kierunkowego prostej $a$.

Jeżeli:
$a \gt 0$, to funkcja jest rosnąca
$a \lt 0$, to funkcja jest malejąca
$a = 0$, to funkcja liniowa jest stała

funkcja rosnąca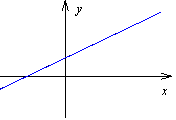

funkcja malejąca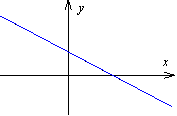

funkcja stała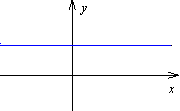

Warunek równoległości i prostopadłości prostych.
Dane są dwie proste:
$k: y = ax + b$
$l: y = cx + d$

Warunek równoległości prostych
Proste w układzie współrzędnych są równoległe wtedy i tylko wtedy, gdy współczynniki kierunkowe tych prostych są równe.
$k || l ⇔ a = c $

Warunek prostopadłości prostych
Proste w układzie współrzędnych są prostopadłe wtedy i tylko wtedy, gdy iloczyn ich współczynników kierunkowych wynosi $-1$.
$k ⊥ l ⇔ a · c = -1$