logowanie

Ekstremum funkcji

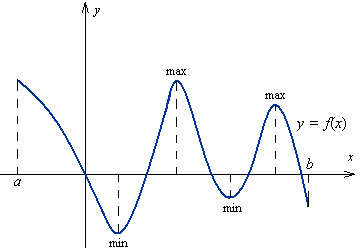
Pojęcia minimum i maksimum lokalnego nie należy mylić z pojęciem wartości najmniejszej i największej w danym przedziale. Maksima i minima to punkty, w których krzywa znajduję się najwyżej i najniżej, jeśli dobrze się przyjrzeć, zauważa się, że tuż przed jest tym samym co tuż po. Ta właściwość charakteryzuje ekstremum.

Niech funkcja f będzie określona w pewnym otoczeniu U punktu x₀.

Mówimy, że funkcja f ma w punkcie x₀:
        minimum lokalne ⇔ ${\displaystyle \underset{\epsilon >0}{\forall }\underset{x\in S(x_0,\epsilon )}{\exists }f\left(x\right)\ge f\left(x_0\right)}$,
        maksimum lokalne ⇔ ${\displaystyle \underset{\epsilon >0}{\forall }\underset{x\in S(x_0,\epsilon )}{\exists }f\left(x\right)\le f\left(x_0\right)}$,
        minimum lokalne właściwe ⇔ ${\displaystyle \underset{\epsilon >0}{\forall }\underset{x\in S(x_0,\epsilon )}{\exists }f\left(x\right)>f\left(x_0\right)}$,
        maksimum lokalne właściwe ⇔ ${\displaystyle \underset{\epsilon >0}{\forall }\underset{x\in S(x_0,\epsilon )}{\exists }f\left(x\right)<f\left(x_0\right)}$,
Minima i maksima noszą wspólną nazwę ekstremów funkcji.

Warunek konieczny istnienia ekstremum (Twierdzenie Fermata)
Jeżeli funkcja f ma w punkcie x₀ ekstremum i pochodną f '(x₀), to f '(x₀) = 0.

Funkcja f może mieć ekstremum jedynie w tych punktach, w których pochodna jest równa zeru, bądĽ w których nie istnieje.

I warunek wystarczający istnienia ekstremum
Jeżeli funkcja f jest ciągła w punkcie x₀ oraz ma pochodną f '(x₀) w pewnym sąsiedztwie S(x₀, δ) = S^-(x₀, δ)∪S⁺(x₀, δ) oraz
a). f '(x₀) < 0 dla każdego x∈S^-(x₀, δ) i f '(x₀) > 0 dla każdego x∈S⁺(x₀, δ), to funkcja f ma w punkcie x₀ minimum (właściwe);
b). f '(x₀) > 0 dla każdego x∈S^-(x₀, δ) i f '(x₀) < 0 dla każdego x∈S⁺(x₀, δ), to funkcja f ma w punkcie x₀ maksimum (właściwe).
Mniej dokładnie określimy, że funkcja f ma w punkcie x₀ ekstremum, jeżeli pochodna przechodząc przez punkt x₀ zmienia znak.

II warunek wystarczający istnienia ekstremum
Jeżeli funkcja f spełnia następujące założenia:
    - ma pochodną f ''(x) w pewnym otoczeniu U(x₀, δ),
    - f ''(x) jest ciągła w punkcie x₀,
    - f '(x₀) = 0 i f ''(x₀) ≠ 0,
to funkcja f ma w punkcie x₀:
    a). minimum właściwe, gdy f ''(x₀) > 0
    b). maksimum właściwe, gdy f ''(x₀) < 0.

© 2024 math.edu.pl      kontakt