Liczby naturalne, zadanie nr 754

Autor	Zadanie / Rozwiązanie
oskar7814 postów: 15	2015-01-06 18:29:47 Dany jest równoległobok ABCD (rysunek poniżej). Na przekątnej AC wybrano punkt X różny od punktu przecięcia przekątnych. Przez punkt X poprowadzono prostą m równoległą do boku AB, przecinającą bok AD w punkcie M i bok BC w punkcie N, oraz prostą n równoległą do boku AD, przecinającą bok AB w punkcie P i bok DC w punkcie Q. Uzasadnij, że czworokąty MXQD i P BNX mają równe pola.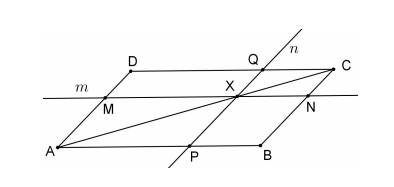

tumor postów: 8070	2015-01-06 18:42:11 Przekątna dzieli równoległobok na dwa trójkąty, które mają oczywiście równe pola. Od trójkąta ACD odejmijmy pola AXM i XCQ Od trójkąta ABC odejmijmy pola APX (identyczne z AXM) i XNC (identyczne z XCQ) Zatem figury, które zostają, mają równe pola.

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj