Planimetria, zadanie nr 1621
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
witam24 post贸w: 14 |  2012-03-27 18:31:341.Dwusieczna k膮ta prostego tr贸jk膮ta prostok膮tnego dzieli przeciwprostok膮tn膮 na odcinki o dl. a i b . Oblicz dl. przyprostok膮tnych . 2.Jedna przek膮tna rombu jest 2 razy d艂u偶sza od drugiej . Wyznacz stosunek obwodu rombu do sumy jego przek膮tnych . 3.Z wierzcho艂ka k膮ta rozwartego r贸wnoleg艂oboku poprowadzono 2 wysoko艣膰i .Wysoko艣ci te tworz膮 k膮t o mierze 50 stopni . Znajd藕 miare k膮ta ostrego r贸wnolegloboku. 4.Ramiona trapezu maj膮 d艂 . 4 i 8 a obw贸d trapezu jest r贸wny 30 . Oblicz d艂 . odcinka 艂膮cz膮cego srodki ramion tego trapezu . 5.Odleg艂o艣膰 艣rodk贸w dw贸ch okr臋g贸w od wierzcho艂ka k膮ta s膮 r贸wne 8 i 12 . Okr臋gi te s膮 stycznie zewn. i ka偶dy z nich jest styczny do obu ramion k膮ta . Oblicz d艂 . ich promieni . 6.Wysoko艣c trapezu r贸wnoramiennego ma d艂. pierwiastek z 6 , a jedna z podstaw jest trzy razy d艂u偶sza od drugiej .Oblisz pole trapezu wi臋dz膮c , 偶e sinus k膮ta ostrego jest r贸wny 0,2 . |
aididas post贸w: 279 | 2012-03-27 18:40:52 2.2a-kr贸tsza przek膮tna 4a-d艂u偶sza przek膮tna bok=$\sqrt{a^{2}+(2a)^{2}}=\sqrt{5a^{2}}$=$a\sqrt{5}$ stosunek=$\frac{4a\sqrt{5}}{2a+4a}=\frac{4a\sqrt{5}}{6a}=\frac{2\sqrt{5}}{3}$ |
marcin2002 post贸w: 484 | 2012-03-27 18:43:49 4. a,b - podstawy 4 i 8 ramiona a+b+4+8=30 a+b=18 ODCINEK 艁膭CZ膭CY 艢RODKI RAMION JEST R脫WNY (a+b)/2 = 18/2=9 |
aididas post贸w: 279 | 2012-03-27 18:48:13 3.Poprzez wysoko艣ci tworzy si臋 deltoid. Mo偶na obliczy膰 k膮t rozwarty (360-90-90-50), kt贸ry wynosi 130 stopni. Dwa tr贸jk膮ty powsta艂e przez podzia艂 s膮 przystaj膮ce, zatem k膮t rozwarty, z kt贸rego opuszczono wysoko艣ci sk艂ada si臋 z 40,50,40 stopni. Teraz wiadomo, 偶e poszukiwany k膮t wynosi 50 stopni (180-90-40). |
marcin2002 post贸w: 484 | 2012-03-27 18:50:23 3. 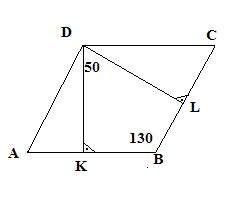 WYSOKO艢CI PADAJ膭 POD K膭TEM PROSTYM SUMA K膭T脫W W CZWOROK膭CIE = 360 DLATEGO w CZWOROK膭CIE DKBL PRZY WIERZCHO艁KU MAMY K膭T 130 STOPNI SKORO JEDEN Z K膭T脫W R脫WNOLEG艁OBOKU MA 130 TO DRUGI MA 50 STOPNI |
aididas post贸w: 279 | 2012-03-27 19:34:45 6. Gdyby wrysowa膰 dwie skrajne wysoko艣ci, to d艂u偶sza podstawa, wynosz膮ca 3a, dzieli si臋 na trzy odcinki o d艂ugo艣ci r贸wnej a. D艂ugo艣膰 a mo偶emy wyliczy膰: sin$\alpha\approx0,2$ ctg$\alpha\approx4,7$ 4,7=$\frac{a}{\sqrt{6}}$ a=4,7$\sqrt{6}$ czyli d艂u偶sza podstawa wynosi: 3$\cdot$4,7$\sqrt{6}$=14,1$\sqrt{6}$ P=$\frac{1}{2}$(a+b)h = $\frac{1}{2}(14,1\sqrt{6}+4,7\sqrt{6})\sqrt{6}$ = $\frac{1}{2}\cdot18,8\sqrt{6}\cdot\sqrt{6}$ = $9,4\sqrt{6}\cdot\sqrt{6}$ = $9,4\cdot6$ = 56,4 Odp.: Pole wynosi oko艂o 56,4. |
agus post贸w: 2387 | 2012-03-27 19:48:42 5. Z twierdzenia Talesa: $\frac{8}{r}=\frac{12}{R}$ 8R=12r z warunk贸w zadania R+r=4 /*12 8R-12r=0 12R+12r=48 20R=48 R=2,4 r=1,6 |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj