Planimetria, zadanie nr 1622
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
witam24 post贸w: 14 |  2012-03-27 22:58:541 D艂ugo艣ci bok贸w tr贸jk膮ta s膮 w stosunku 2:3:4. Oblicz cosinus najwiekszego kata tego tr贸jk膮ta . 2. Rami臋 trojkata rownoramiennego ma dl. b, a k膮t przy podstawie ma miare $\alpha$. Wyznacz d艂 promienia a)okregu opisanego na tr贸jkacie b) okregu wpisanego w tr贸jk膮t 3. Jeden z k膮t贸w tr贸jk膮a o obwodzie 6 ma miar臋 60 stopni , a stosunek d艂ugo艣膰i bok贸w zawartych w ramionach tego k膮ta jest r贸wny 1:2 . Oblicz pole tr贸jk膮ta . 4.D艂u偶sza przek膮tna r贸wnoleg艂oboku o k膮cie ostrym 60 stopni , ma d艂ugo艣膰 3$\sqrt{7}$. r贸偶nica d艂ugo艣ci jego bok贸w wynosi 3. Oblicz pole tego r贸wnoleg艂oboku i d艂ugo艣c kr贸tszej przek膮tnej . 5. Odcinek 艂膮cz膮cy 艣rodki ramion trapezu opisanego na okr臋gu o promieniu 1 ma d艂ugo艣c 4 . Oblicz obw贸d i pole tego trapezu . 6.Na okr臋gu o promieniu r opisano trapez prostok膮tny , kt贸rego najkr贸tszy bok ma d艂. $\frac{3}{2}$r . Oblicz pole tego trapezu oraz stosunek jego d艂ugo艣ci przek膮tnych. 7.Promie艅 okr臋gu wpisanego w wycinek ko艂a o k膮cie 艣rodkowym 60 st. ma d艂. 2 . Oblicz pole powierzchni tego wycinka . |
marcin2002 post贸w: 484 | 2012-03-27 23:10:41 1 NAJWI臉KSZY K膭T JEST NAPRZECIW NAJD艁U呕SZEGO BOKU boki : 2x,3x,4x $(4x)^2=(2x)^2+(3x)^2-2\cdot2x\cdot3x\cdot cos\alpha$ $16x^{2}=4x^{2}+9x^{2}-12x^{2}cos\alpha$ $3x^{2}=12x^{2}cos\alpha$ $\frac{1}{4}=cos\alpha$ |
marcin2002 post贸w: 484 | 2012-03-27 23:20:38 3. boki zawarte w ramionach k膮ta : x,2x bok naprzeciw k膮ta : a $a^{2}=x^{2}+(2x)^2-2\cdot x\cdot2x\cdot cos60$ $a^{2}=x^{2}+4x^2-4x^{2}cos60$ $a^{2}=5x^{2}-4x^{2}\cdot\frac{1}{2}$ $a^2=5x^{2}-2x^{2}$ $a^2=3x^{2}$ $a=x\sqrt{3}$ $x+2x+x\sqrt{3}=6$ $3x+x\sqrt{3}=6$ $x(3+\sqrt{3})=6$ $x=\frac{6}{3+\sqrt{3}}$ $x=3-\sqrt{3}$ $P=\frac{1}{2}x\cdot2x\cdot sin60$ $P=x^{2}\cdot\frac{\sqrt{3}}{2}$ $P=(3-\sqrt{3})^2\cdot\frac{\sqrt{3}}{2}$ $P=(12-6\sqrt{3})\cdot\frac{\sqrt{3}}{2}$ $P=6\sqrt{3}-9$ |
sylwia94z post贸w: 134 | 2012-03-27 23:20:55 7.  sin30=$\frac{2}{x}$ $\frac{1}{2}=\frac{2}{x}$ x=4 r=2+4=6 $P_{wycinka}=\frac{60}{360}\cdot\pi\cdot6^{2}=6\pi$ |
marcin2002 post贸w: 484 | 2012-03-27 23:23:25 5 $\frac{a+b}{2}=4$ a+b=8 a,b - podstawy c - rami臋 z warunku opisywalno艣ci czworok膮ta na okr臋gu a+b=c+c 8=2c c=4 OBW=16 艣rednica okr臋gu jest wysoko艣ci膮 trapezy h=2r=2 $P=\frac{8\cdot2}{2}=8$ |
doris125 post贸w: 12 | 2012-03-27 23:29:36 ZADANIE 6 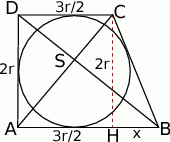 Gdy $HB=x$ to mamy: $AD+BC=AB+CD$ $2r+BC=1,5r+x+1,5r$ $BC=r+x$ $HB^{2}+HC^{2}=BC^{2}$ $x^{2}+4r^{2}=(x+r)^{2}$ $x^{2}+4r^{2}=x^{2}+2xr+r^{2}$ $2xr=3r^{2}$ $x=\frac{3r}{2}$ Pole trapezu: $P=\frac{AB+CD}{2}\cdot 2r=\frac{9}{2}r^{2}$ $AC=\sqrt{AH^{2}+HC^{2}}=\frac{5r}{2}$ $BD=\sqrt{AB^{2}+AD^{2}}=r\sqrt{13}$ szukany stosunek: $\frac{BD}{AC}=\frac{r\sqrt{13}}{\frac{5r}{2}}=\frac{2\sqrt{13}}{5}$ Wiadomo艣膰 by艂a modyfikowana 2012-03-27 23:29:55 przez doris125 |
agus post贸w: 2387 | 2012-03-27 23:58:25 4. x, x+3 boki r贸wnoleg艂oboku h- wysoko艣膰 r贸wnoleg艂oboku poprowadzona do boku x+3 p-kr贸tsza przek膮tna r贸wnoleg艂oboku k膮t rozwarty r贸wnoleg艂oboku ma $120^{0}$ $(3\sqrt{7})^{2}$=$x^{2}$+$(x+3)^{2}$-2x(x+3)cos$120^{0}$ cos$120^{0}$=-cos$60^{0}$=-$\frac{1}{2}$ 63=$x^{2}+x^{2}$+6x+9+$x^{2}$+3x 3$x^{2}$+9x-54=0 /:3 $x^{2}$+3x-18=0 $\triangle$=9+72=81 $\sqrt{\triangle}$=9 x=$\frac{-3+9}{2}$=3 x+3=6 $\frac{h}{x}$=sin$60^{0}$=$\frac{\sqrt{3}}{2}$ h=$\frac{3\sqrt{3}}{2}$ P=6$\cdot$$\frac{\sqrt{3}}{2}$=9$\sqrt{3}$ $p^{2}$=$3^{2}+6^{2}$-2$ \cdot3 \cdot 6 \cdot cos60^{0}$=9+36-18=27 p=3$\sqrt{3}$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj