Inne, zadanie nr 1725
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
masmak post贸w: 28 |  2012-04-16 18:31:0320. Punkt A(0,-5) , B(4,3) i C(-1,3) sa wierzcholkami trapezu rownoramiennego ABCD o podstawach AB i CD. Wyznacz wierzcholek D i oblicz pole trapezu. 21. Oblicz objetosc ostroslupa prawidlowego czworokatnego majac dlugosc krawedzi podstawy 6 i miare 120 stopni kata miedzy dwiema sasiednimi scianami bocznymi. 22. Pole sciany bocznej ostroslupa prawidlowego czworokatnego jest rowne S. Kat plaski przy wierzcholku ostroslupa ma miare 2 $ \alpha $. Oblicz objetosc ostroslupa. |
agus post贸w: 2387 | 2012-04-16 20:26:15 22. a-kraw臋d藕 podstawy h-wysoko艣膰 艣ciany bocznej tg$\alpha$=$\frac{\frac{1}{2}a}{h}$=$\frac{a}{2h}$ a=2htg$\alpha$(1) $\frac{1}{2}$ah=S ah=2S h=$\frac{2S}{h}$ (2) podstawiamy (2) do (1) a=$\frac{4S}{a}tg\alpha$ $a^{2}$=4Stg$\alpha$(3) a=2$\sqrt{Stg\alpha}$(4) podstawiamy (4) do (2) h=$\frac{2S}{2\sqrt{Stg\alpha}}$=$\frac{\sqrt{Stg\alpha}}{tg\alpha}$(5) H-wysoko艣膰 ostros艂upa $\frac{1}{2}$a=$\sqrt{Stg\alpha}$ $H^{2}=h^{2}-(\frac{1}{2}a)^{2}$=$\frac{Stg\alpha}{tg^{2}\alpha}$-Stg$\alpha$=$\frac{Stg\alpha-Stg^{2}\alpha}{tg^{2}\alpha}$ H=$\frac{\sqrt{Stg\alpha(1-tg\alpha)}}{tg\alpha}$ V=$\frac{1}{3}a^{2}H$=$\frac{1}{3}4Stg\alpha$$\frac{\sqrt{Stg\alpha(1-tg\alpha)}}{tg\alpha}$= =$\frac{4}{3}$S$\sqrt{Stg\alpha(1-tg\alpha)}$ |
agus post贸w: 2387 | 2012-04-16 21:36:53 20. prosta AB y= $\frac{-5-3}{0-4}$x-5=2x-5 prosta CD || prosta AB y=2x+b C=(-1,3) 3=-2+b b=5 y=2x+5 punkt D=(x,y)=(x,2x+5) d艂ugo艣膰 CB=$\sqrt{(-1-4)^{2}+(3-3)^{2}}$=5 AD=5 AD=$\sqrt{x^{2}+(2x+5+5)^{2}}$=$\sqrt{5x^{2}+40x+100}$=5 $5x^{2}$+40x+100-25=0 /:5 $x^{2}$+8x+15=0 $\triangle$=64-60=4 $\sqrt{\triangle}$=2 x=$\frac{-8-2}{2}$=-5, y= 2*(-5)+5=-5 lub x=$\frac{-8+2}{2}$=-3, y =2*(-3)+5=-1 wybieramy punkt bli偶szy C, czyli D=(-3,-1) |
rafal post贸w: 248 | 2012-04-17 18:26:25 20. 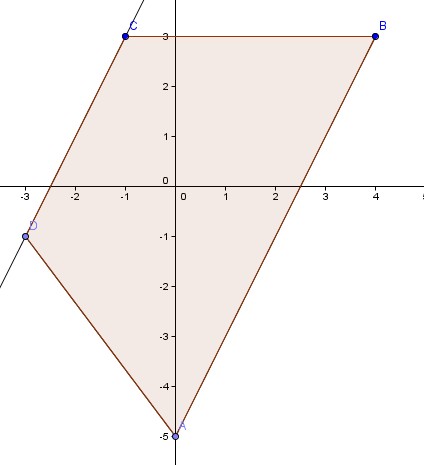 pole to 30 |
aididas post贸w: 279 | 2012-04-17 18:52:55 21.Skoro k膮t mi臋dzy przeciwnymi 艣cianami bocznymi wynosi $120^{\circ}$, to wysoko艣膰 opuszczona na podstaw臋 dzieli przekr贸j ostros艂upa na dwa tr贸jk膮ty o k膮tach $60^{\circ}$,$30^{\circ}$ i $90^{\circ}$. Wiadomo, 偶e d艂ugo艣ci bok贸w tr贸jk膮t贸w przy podstawie ostros艂upa s膮 dwa razy mniejsze ni偶 d艂ugo艣膰 boku kwadratu w podstawie, czyli 3. Ta d艂ugo艣膰 stanowi jakby wysoko艣膰 w tr贸jk膮cie r贸wnobocznym, gdzie wysoko艣膰 ostros艂upa stanowi po艂ow臋 d艂ugo艣ci boku wyobra偶onego tr贸jk膮ta r贸wnobocznego. Mamy wi臋c r贸wnanie: $\left\{\begin{matrix} H=\frac{1}{2}a \\ 3=\frac{a\sqrt{3}}{2} \end{matrix}\right.$ $\left\{\begin{matrix} a=2H \\ 3=\frac{2H\sqrt{3}}{2} \end{matrix}\right.$ $\left\{\begin{matrix} a=2H \\ 3=H\sqrt{3} \end{matrix}\right.$ $\left\{\begin{matrix} a=2H \\ H=\frac{3}{\sqrt{3}} \end{matrix}\right.$ $\left\{\begin{matrix} a=2H \\ H=\frac{3\sqrt{3}}{3} \end{matrix}\right.$ $\left\{\begin{matrix} a=2H \\ H=\sqrt{3} \end{matrix}\right.$ Teraz wyliczamy obj臋to艣膰 ostros艂upa: $V=\frac{1}{3}\cdot P_{p}\cdot H$ $V=\frac{1}{3}\cdot 6^{2}\cdot \sqrt{3}$ $V=\frac{1}{3}\cdot 36\cdot \sqrt{3}$ $V=12\cdot \sqrt{3}$ $V=12\sqrt{3}$ Odp.: Obj臋to艣膰 ostros艂upa wynosi$12\sqrt{3}$. |
witam24 post贸w: 14 | 2012-04-18 23:47:31 \"Wiadomo, 偶e d艂ugo艣ci bok贸w tr贸jk膮t贸w przy podstawie ostros艂upa s膮 dwa razy mniejsze ni偶 d艂ugo艣膰 boku kwadratu w podstawie, czyli 3.\" nie moge tego zrozumie膰 zadania . Gdzie jest ten tr贸jk膮t r贸wnoboczny ? |
aididas post贸w: 279 | 2012-04-19 16:16:35 Tr贸jk膮t powsta艂y przy opuszczeniu wysoko艣ci stanowi po艂ow臋 tr贸jk膮ta r贸wnobocznego. Wynika to z tego, i偶 powsta艂y tr贸jk膮t ma k膮ty $90^{\circ}$,$60^{\circ}$ i $30^{\circ}$. Dobrze to wida膰, gdy rozrysujesz sobie ca艂y tok rozwi膮zania tego zadania. |
witam24 post贸w: 14 | 2012-04-20 23:37:56 Nie rozumiem nadal dalszej cz臋s膰i wyja艣niania ;p moim zdaniem co艣 tu jest nie tak w tym rozwi膮zaniu . |
agus post贸w: 2387 | 2012-04-21 10:36:44 21. K膮t mi臋dzy s膮siednimi 艣cianami bocznymi to k膮t mi臋dzy wysoko艣ciami 艣cian (h) poprowadzonymi do kraw臋dzi bocznej. Mamy zatem tr贸jk膮t r贸wnoramienny o podstawie p (przek膮tna podstawy, przek膮tna kwadratu) i ramionach h i k膮cie mi臋dzy ramionami $120^{0}$. Obliczamy h $\frac{\frac{1}{2}p}{h}=sin60^{0}$ $\frac{3\sqrt{2}}{h}=\frac{\sqrt{3}}{2}$ h=2$\sqrt{6}$ na 艣cianie bocznej h-wysoko艣膰 poprowadzona do kraw臋dzi bocznej $h_{s}$-wysoko艣膰 艣ciany boczej 6-kraw臋d藕 podstawy tr贸jk膮ty prostok膮tne o bokach:$h_{s}$,3 i kraw臋d藕 boczna oraz h,x i 6 s膮 podobne (maj膮 takie same k膮ty) $x^{2}=6^{2}-(2\sqrt{6})^{2}$=12 x=2$\sqrt{3}$ z podobie艅stwa tr贸jk膮t贸w $\frac{2\sqrt{6}}{2\sqrt{3}}=\frac{h_{s}}{3}$ $h_{s}$=3$\sqrt{2}$ H-wysoko艣膰 ostros艂upa,a-kraw臋d藕 podstawy $H^{2}=h^{2}-(\frac{1}{2}a)^{2}$ $H^{2}=(3\sqrt{2})^{2}-3^{2}$=9 H=3 V=$\frac{1}{3}\cdot 6^{2}\cdot 3$=36 |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj