Liczby rzeczywiste, zadanie nr 1865
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
supergosc4 post贸w: 11 |  2012-06-04 18:08:16Zbadaj liczb臋 rozwi膮za艅 r贸wnania $a=\sqrt{2|x|-x^{2}} $w zale偶no艣ci od warto艣ci parametru a . |
irena post贸w: 2636 | 2012-06-04 22:28:57 $\sqrt{2|x|-x^2}=a$ $x^2\le2|x|$ $x\in<;-2; 2>$ Narysuj parabol臋 o r贸wnaniu $y=-x^2+2x$ dla $x\in<;0; 2>$. Odbij t臋 cz臋艣膰 paraboli symetrycznie wzgl臋dem osi OY. Otrzymasz wykres funkcji $y=-x^2+2|x|$. Poszukuje si臋 wsp贸lnych punkt贸w tego wykresu z prost膮 o r贸wnaniu $y=a^2$. a musi by膰 liczb膮 nieujemn膮. Dla $a\in(-\infty; 0)\cup(1; \infty)$ r贸wnanie nie ma rozwi膮za艅. Dla $a=1$ r贸wnanie ma 2 rozwi膮zania. Dla $a=0$ r贸wnanie ma 3 rozwi膮zania. Dla $a\in(0;1)$ r贸wnanie ma 4 rozwi膮zania. Wiadomo艣膰 by艂a modyfikowana 2012-06-05 10:05:34 przez irena |
agus post贸w: 2387 | 2012-06-04 22:58:28 2|x|-$x^{2}\ge0$ $x^{2}-2|x|\le0$ 1)x$\ge$0 $x^{2}-2x\le0$ x(x-2)$\le0$ x$\in<0;2>$ 2)x<0 $x^{2}+2x\le0$ x(x+2)$\le$0 x$\in <-2;0)$ a$\ge$0 (bo to pierwiastek kwadratowy) $a^{2}=2|x|-x^{2}$ $x^{2}-2|x|+a^{2}=0$ 1)$\triangle$=4-4$a^{2}>0$ 4$a^{2}-4<0$ $a^{2}-1<0$ (a+1)(a-1)<0 bior膮c pod uwag臋 za艂o偶enie: a$\in (0;1)$ $x^{2}-2x+a^{2}=0$ x$\in<0;2>$ $x_{1}+x_{2}$=1 $x_{1}\cdot x_{2}=a^{2}$ (2 rozwi膮zania) $x^{2}+2x+a^{2}=0$ x$\in<-2;0)$ $x_{1}+x_{2}$=-1 $x_{1}\cdot x_{2}=a^{2}$ (2 rozwi膮zania) zatem, dla a$\in(0;1)$ r贸wnanie ma 4 rozwi膮zania 2)$\triangle$=4-4$a^{2}$=0 bior膮c pod uwag臋 za艂o偶enie: a=1 (r贸wnanie $x^{2}-2|x|+1=0$, czyli r贸wnania $x^{2}-2x+1=0 $ oraz $x^{2}+2x+1=0$; maj膮 rozwi膮zania x=1, x=-1, czyli 2 rozwi膮zania) 3)$\triangle$=4-4$a^{2}$<0 bior膮c pod uwag臋 za艂o偶enie:a$\in(1;+\infty)$ (r贸wnanie nie ma rozwi膮zania) Wiadomo艣膰 by艂a modyfikowana 2012-06-04 23:05:28 przez agus |
supergosc4 post贸w: 11 | 2012-06-05 00:09:14 wysz艂o mi ,偶e 0 rozwi膮za艅 dla $(-\infty,-1)\cup(1,+\infty)$ oraz 偶e dla 2 rozwi膮za艅 a $a\in {1,-1}$??? po narysowaniu funkcji $-x^2+2|x|$ wychodzi ,偶e (przyjmuj膮c $t=a^2$) 0 dla t>1 2 dla t={1} i t<0 3 dla t=0 4 dla 0>t>1 no to 0 dla -1<a>1 2 dla a=1 -1 |
irena post贸w: 2636 | 2012-06-05 10:08:04 Liczba a jest r贸wna warto艣ci pierwiastka kwadratowego, musi by膰 wi臋c liczb膮 nieujemn膮. Je艣li a<0, to rozwi膮za艅 nie ma na pewno. |
supergosc4 post贸w: 11 | 2012-06-05 18:05:36 czyli -2=$\sqrt{2|x|-x^2}$ b臋dzie zawsze sprzeczne??? |
marcin2002 post贸w: 484 | 2012-06-05 18:30:28 tak, poniewa偶 pierwiastek drugiego stopnia jest zawsze liczb膮 dodatni膮 a -2 jest ujemne |
agus post贸w: 2387 | 2012-06-05 18:31:16 Tak, r贸wnanie jak wy偶ej jest sprzeczne. a$\ge$0 Do mojego rozwi膮zania nale偶y doda膰 jeszcze a=0 wtedy $x^{2}-2|x|=0$ czyli $x^{2}$-2x=0, x$\in<0;2>$ x(x-2)=0 rozwi膮zania: x=0,x=2 lub $x^{2}+2x=0$,x$\in<-2;0)$ x(x+2)=0 rozwi膮zanie: x=-2 zatem, dla a=0 r贸wnanie ma 3 rozwi膮zania Podsumowuj膮c: a=0, 3 rozwi膮zania a$\in(0,1)$, 4 rozwi膮zania a=1, 2 rozwi膮zania a$\in(1,+\infty)$, 0 rozwi膮za艅 (a jest liczb膮 nieujemn膮) Ponadto, rozwi膮zania r贸wnania nale偶膮 do przedzia艂u <-2,2>. |
supergosc4 post贸w: 11 | 2012-06-06 18:27:22 a np. dla $m^2+||x-3||=3$ $m^2=3-||x-3|-3|$ 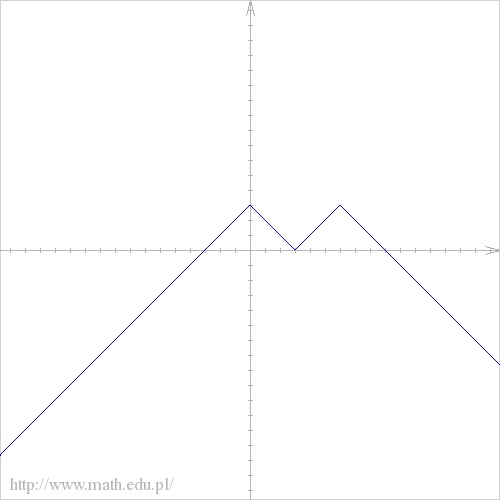 czyli : $0dla m^2 = (-\infty,3)$ $2 dla m^2 ={3}i(-\infty,0)$ $3 dla m^2 ={0}$ $4 dla m^2 =(0,3)$ wi臋c $m=\sqrt{3-||x-3|-3|}$ $m^2<3$ $m^2-3<0$ $3>m>-3$ ale m>0 czyli 偶e 0 dla m$(-\infty,0)(\sqrt{3},\infty)$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj