Wyra偶enia algebraiczne, zadanie nr 1930
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
sylwia551 post贸w: 25 |  2012-09-04 17:55:02Sprawdz, 偶e podana liczba jest pierwiastkiem r贸wnania, a nast臋pnie znajd藕 jego pozosta艂e pierwiastki: $x^{4}$+$8x^{3}$+$19x^{2}$+32x+60=0 ; -5 Wiadomo艣膰 by艂a modyfikowana 2012-09-04 18:03:45 przez sylwia551 |
pm12 post贸w: 493 | 2012-09-04 19:27:49 potraktujmy napis po lewej stronie r贸wno艣ci jako f(x). wtedy f(-5)=625-1000+475-160+60=0 , a wi臋c liczba -5 to pierwiastek. po wykonaniu schematu hornera (dla dwumianu (x+5)) mamy $x^{3}$ + 3$x^{2}$ + 4x + 12 = 0 po pogrupowaniu (pierwszy wyraz z drugim, a trzeci z czwartym) wyraz贸w mamy (x+3)($x^{2}$+3)=0 jedynym rzeczywistym pierwiastkiem tego r贸wnania jest x=-3 |
abcdefgh post贸w: 1255 | 2012-09-06 01:54:09 $x^4+8x^3+19x^2+32x+60=0$ $w(x)=(x+5)(x^3+3x^2+4x+12)$ 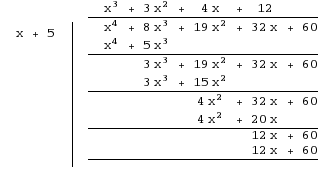 $g(x)=x^3+3x^2+4x+12$ $g(-3)=-27+27-12+12=0$ 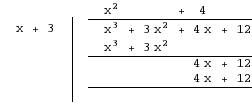 $w(x)=(x+5)(x+3)(x^2+4)$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj