Trygonometria, zadanie nr 2574
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
primrose post贸w: 62 |  2013-02-26 19:05:16Funkcja g(m) oznacza liczb臋 rozwi膮za艅 r贸wnania $| 2cos (|x|) - 1 | = m $ w przedziale <-2\pi, 2\pi> w zale偶no艣ci od parametru m. Wykonaj wykres funkcji g(m). Z g贸ry dzi臋kuj臋 za pomoc :) |
lukipuki post贸w: 29 | 2013-03-04 17:39:16 Oto wykres funkcji $f(x)=|2cos(|x|)-1| $ : 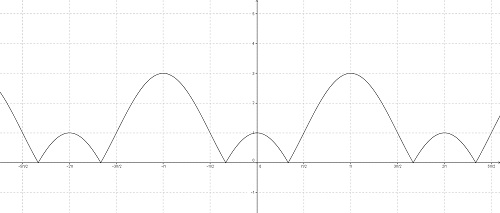 Je偶eli naszkicujemy sobie ten wykres, to w prosty spos贸b mo偶emy naszkicowa膰 wykres $m=|2cos(|x|)-1| $ \"m\" w tym zapisie funkcji jest warto艣ci膮 funkcji $f(x)$ i zarazem argumentem funkcji $g(m)$. Dlatego, aby naszkicowa膰 wykres funkcji $g(m)$ musimy rozpisa膰 sobie dla jakiego m ile jest rozwi膮za艅, czyli ile razy przetniemy wykres prost膮 poziom膮 na ka偶dym z jego odcink贸w. I tak: dla $m\in(-\infty;0)\cup(3;+\infty)$ mamy 0 rozwi膮za艅 dla $m=3$ mamy 2 rozwi膮zania dla $m\in(1;3) $ i $ m=0$ mamy 4 rozwi膮zania dla $m=1$ mamy 7 rozwi膮za艅 dla $m\in(0;1)$ mamy 8 rozwi膮za艅. Teraz posiadaj膮c takie dane mo偶emy swobodnie pozaznacza膰 te punkty oraz odcinki i inne linie w uk艂adzie wsp贸艂rz臋dnych. Nale偶y uwa偶a膰 na to, gdzie nasze \"k贸艂ka\" maj膮 by膰 zamalowane, a gdzie nie!(je偶eli mamy nawias otwarty \"( )\" to k贸艂ko pozostawiamy puste, a je偶eli nawias jest domkni臋ty \"< >\" to k贸艂ko zamalowujemy. Wykres $m=|2cos(|x|)-1| $ wygl膮da nast臋puj膮co:  |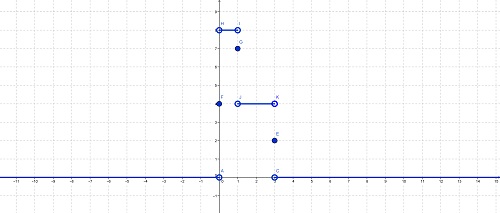
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj