Liczby rzeczywiste, zadanie nr 2590
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
kokabango post贸w: 144 |  2013-03-01 20:43:09zad 13. Oblicz odleg艂o艣膰 punktu A os 艣rodka odcinka BC , gdzie A=(1,3) , B(4,7) , C(-2,-3). Prosz臋 o wszystkie obliczenia z tego zadania. Karola |
lukipuki post贸w: 29 | 2013-03-02 21:48:54 Oto jak ta sytuacja wygl膮da na p艂aszczy藕nie kartezja艅skiej: 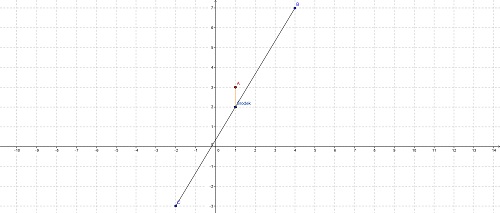 Aby wyliczy膰 wsp贸艂rz臋dne 艣rodka nale偶y wykona膰 dwa dzia艂ania (r贸偶nice): *wsp贸艂rz臋dne 艣rodka symetrii oznacz臋 jako S=(x;y)* 1.R贸偶nica - aby otrzyma膰 wsp贸艂rz臋dn膮 x= $\frac{4+(-2)}{2}$ z czego otrzymujemy \"1\" , nast臋pnie obliczamy y=$\frac{7+(-3)}{2}$ z czego otrzymujemy \"2\". Dlatego S=(1;2). Teraz mo偶emy obliczy膰 d艂ugo艣膰 odcinka |AS| ze wzoru na d艂ugo艣膰 odcinka $d=\sqrt{(x_{a}-x_{s})^{2}+(y_{a}-y_{s})^{2}}$ Podstawiamy punkty do wzrou: $d=\sqrt{(1-1)^{2}+(3-2)^{2}}= 1$ <<< oto wynik. |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj