Geometria, zadanie nr 2929
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
adamksiazek post贸w: 5 |  2013-05-20 17:39:15Zad.4. K膮t ostry r贸wnoleg艂oboku ma miar臋 60 stopni. Stosunek kwadrat贸w d艂ugo艣ci jego przek膮tnych jest r贸wny 0,(3). Wyka偶, 偶e ten r贸wnoleg艂obok jest rombem. Zad.5. W trapezie opisanym na okr臋gu d艂ugo艣ci ramion s膮 odpowiednio r贸wne 9 i 15. Odcinek 艂膮cz膮cy 艣rodki tych ramion dzieli go na dwa trapezy, kt贸rych stosunek p贸l jest r贸wny 0,6. Wyznacz d艂ugo艣ci podstaw trapezu oraz pole ko艂a wpisanego w ten trapez. Zad.6. Figur臋 o r贸wnaniu x2 + y2 + 8x - 8y + 30 = 0 przekszta艂cono w jednok艂adno艣ci wzgl臋dem punktu O = (-2, 3) i skali k = -2. Wyznacz r贸wnanie otrzymanej figury. Co to za figura? Wykonaj odpowiedni rysunek w uk艂adzie wsp贸艂rz臋dnych. |
abcdefgh post贸w: 1255 | 2013-05-20 21:10:48 zad.5 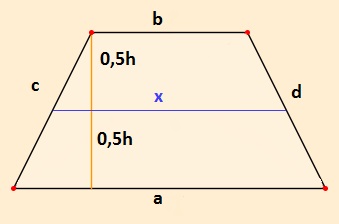 Okr膮g wpisany w trapez ma pewn膮 w艂asno艣膰: suma bok贸w le偶膮cych naprzeciw siebie s膮 r贸wne. czyli: a+b=c+d 9+15=a+b 24=a+b a=24-b x-艣rodek 艂膮cz膮cy ramiona $x=\frac{a+b}{2}=\frac{24-b+b}{2}=12$ $P_{1}$-pole pierwszego trapezu o podstawach b,x $P_{2}$-pole pierwszego trapezu o podstawach a,x $\frac{0,5*0,5h*(b+x)}{0,5*0,5*h*(a+x)}=\frac{6}{10}$ $\frac{b+12}{24-b+12}=\frac{6}{10}$ 10b+120=216-6b 16b=96 b=6 a=18 $P_{1}=0,25h*(6+12)=4,5h$ $P_{2}=0,25h(12+18)=7,5h$ $\frac{4,5h}{7,5h}=0,6$ $0,6h=0,6$ $h=1$ r=0,5h=0,5 P=$\pi*r^2=\pi0,25$ Wiadomo艣膰 by艂a modyfikowana 2013-05-20 21:14:32 przez abcdefgh |
agus post贸w: 2387 | 2013-05-23 22:26:50 4) p,q-przek膮tne r贸wnoleg艂oboku; a,b-boki r贸wnolegloboku z tw. cosinus贸w $p^{2}=a^{2}+b^{2}-2abcos120=a^{2}+b^{2}+ab$ $q^{2}=a^{2}+b^{2}-2abcos60=a^{2}+b^{2}-ab$ $\frac{q^{2}}{p^{2}}=\frac{a^{2}+b^{2}-ab}{a^{2}+b^{2}+ab}=\frac{1}{3}$ $3a^{2}+3b^{2}-3ab=a^{2}+b^{2}+ab$ $2a^{2}+2b^{2}-4ab=0$ $a^{2}+b^{2}-2ab=0$ $(a-b)^{2}=0$ a=b Zatem r贸wnoleg艂obok jest rombem |
agus post贸w: 2387 | 2013-05-25 00:33:31 6. Dana figura to okr膮g a=-4 b=4 $r^{2}=(-4)^{2}+4^{2}-30=2$ r=$\sqrt{2}$ inne r贸wnanie danego okr臋gu $(x+4)^{2}+(y-4)^{2}=2$(okr膮g o 艣rodku (-4,4) i promieniu $\sqrt{2}$) okr膮g po przekszta艂ceniu przez jednok艂adno艣膰 ma promie艅 2 razy wi臋kszy, a 艣rodek okr臋gu le偶y na prostej przechodz膮cej przez punkty (-4,4) i (-2,3), po drugiej stronie punktu (-2,3) ni偶 (-4,4) i w odleg艂o艣ci 2 razy wi臋kszej ni偶 odleg艂o艣膰 od (-4,4) do (-2,3) r\'=2$\sqrt{2}$ $r\'^{2}=8$ odleg艂o艣膰 od (-4,4) do (-2,3) $\sqrt{(-4+2)^{2}+(4-3)^{2}}=\sqrt{5}$ odleg艂o艣膰 od (-2,3) do (x,y) (艣rodka szukanego okr臋gu) $\sqrt{(x+2)^{2}+(y-3)^{2}}=2\sqrt{5}$ $(x+2)^{2}+(y-3)^{2}=20$(1) r贸wnanie prostej przechodz膮cej przez (-4,4) i (-2,3) 4=-4a+b 3=-2a+b po odj臋ciu stronami a=-$\frac{1}{2}$ b=2 y=-$\frac{1}{2}$x+2 (2) wstawiaj膮c (2) do (1) i porz膮dkuj膮c otrzymujemy $x^{2}$+4x-12=0 $\triangle$ =64 $\sqrt{\triangle}$=8 x1=-6 x2=2 po podstawieniu do (2) y1=5 y2=1 (-6,5),(2,1) punkt (2,1) le偶y po drugiej stronie (-2,3) ni偶 (-4,4) r贸wnanie szukanego okr臋gu $(x-2)^{2}+(y-1)^{2}=8$ (okr膮g o 艣rodku (2,1) i promieniu 2$\sqrt{2}$) |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj