Planimetria, zadanie nr 2960
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
mateusz1234 post贸w: 65 |  2013-06-01 11:39:15D艂ugo艣ci dwu s膮siednich bok贸w r贸wnoleg艂oboku r贸偶ni膮 si臋 o 3, k膮t ostry ma miar臋 $60$, a d艂u偶sza przek膮tna $3\sqrt{7}$. Oblicz pole tego r贸wnoleg艂oboku i kr贸tszej przek膮tnej. |
abcdefgh post贸w: 1255 | 2013-06-01 19:42:54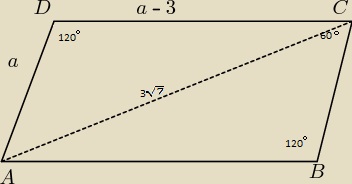 tr贸jk膮t ACD twierdzenie cosinus贸w $(3\sqrt{7})^2=a^2+(a-3)^2-2*a(a-3)*cos120^{o}$ $63=a^2+a^2-6a+9-2(a^2-3a)*cos(180^{o}-60^{o})$ $63=2a^2-6a+9-2(a^2-3a)*(-cos60^{o})$ $63=2a^2-6a+9-2(a^2-3a)*\frac{-1}{2}$ $63=2a^2-6a+9-a^2+3a$ $63=a^2-3a+9$ $a^2-3a-54=0$ $\delta=225$ $\sqrt{\delta}=15$ $a_{1}=9$ $a_{2}=-6$ a<0 sprzeczno艣c $a=9$ $a-3=6$ $P=6*9*sin60^{o}$ $P=54*\frac{\sqrt{3}}{2}=27\sqrt{3}$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj