Planimetria, zadanie nr 2961
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
mateusz1234 post贸w: 65 |  2013-06-01 11:42:16Rami臋 tr贸jk膮ta r贸wnoramiennego jest dwa razy d艂u偶sze od podstawy. Suma promieni okr臋g贸w wpisanego w tr贸jk膮t i opisanego na tym tr贸jk膮cie jest r贸wna 11. Oblicz d艂ugo艣膰 podstawy tr贸jk膮ta. |
abcdefgh post贸w: 1255 | 2013-06-01 21:39:19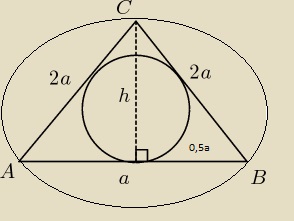 $h^2=4a^2-\frac{1}{4}a^2=\frac{15}{4}a^2$ $h=\frac{\sqrt{15}}{2}a$ $P=\frac{\sqrt{15}}{4}a^2$ $r=\frac{2P}{a+b+b}$ r=$\frac{2\frac{\sqrt{15}a^2}{4}}{5a}=\frac{\sqrt{15}}{10}$ $R=\frac{abc}{4P}$ $R=\frac{4a^3}{4*\frac{\sqrt{15}a^2}{4}}$ $R=\frac{4a}{\sqrt{15}}$ r+R=11 $\frac{\sqrt{15}a^2}{10}$+$\frac{4a}{\sqrt{15}}$=11 $\frac{15a+40a}{10\sqrt{15}}=11$ $55a=110\sqrt{15}$ $a=2\sqrt{15}$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj