Planimetria, zadanie nr 2963
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
mateusz1234 post贸w: 65 |  2013-06-01 11:51:28D艂ugo艣ci bok贸w czworok膮ta ABCD wpisanego w okr膮g wynosz膮 |AB|=1, |BC|=2, |CD|=3, |AD|=4. Oblicz cosinus k膮ta zawartego mi臋dzy najkr贸tszymi bokami. |
abcdefgh post贸w: 1255 | 2013-06-01 19:05:25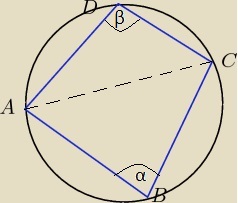 a=AB b=BC c=CD d=DA Skorzystamy z twierdzenia Homera P=$\frac{1}{2}*\sqrt{(p-a)(p-b)(p-c)(p-d)}$ $p=\frac{1}{2}(a+b+c+d)$ $p=\frac{1}{2}(1+2+3+4)=\frac{1}{2}*10=5$ $P=\sqrt{(5-1)(5-2)(5-3)(5-4)}=$$(4*3*2*1)=\sqrt{24}=2\sqrt{6}$ $2\sqrt{6}=P_{ABC}+P_{ACD}$ $P_{ABC}=\frac{1}{2}*1*2*sin\alpha=sin\alpha$ $P_{ACD}=\frac{1}{2}*3*4*sin\beta=6sin\beta$ $2\sqrt{6}=sin\alpha+6sin\beta$ Pami臋tajmy 偶e je偶eli czworok膮t jest wpisany w okr膮g to jest katy le偶膮ce naprzeciwko siebie s膮 r贸wne $180^{o}$ $\alpha+\beta=180^{o}$ $\alpha=180^{o}-\beta$ $2\sqrt{6}=sin\alpha+6sin(180^{o}-\alpha)$ $2\sqrt{6}=sin\alpha+6sin\alpha$ $2\sqrt{6}=7sin\alpha$ $sin\alpha=\frac{2\sqrt{6}}{7}$ $cos\alpha=\sqrt{1-\frac{24}{49}}=\frac{5}{7}$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj