Inne, zadanie nr 3381
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
zuzannaruda post贸w: 4 |  2013-11-11 13:33:19Witam,prosz臋 o wyt艂umaczenie krok po kroku algorytmu, zw艂aszcza Witam, prosz臋 o wyt艂umaczenie krok po kroku algorytmu, zw艂aszcza warunku i=100, nie rozumiem tego dlaczego jest taki warunek. Wiem ze tam jest b艂膮d , nie powinno by膰 dwa razy nie, po lewej musi by膰 tak, ale i tak nic mi to nie przeja艣ni艂o prosz臋 o jak najszybsz膮 rozpisk臋 Jestem podstarza艂膮 uczennic膮, ucz臋 si臋 sama, nie ma kto mi pom贸c wi臋c licz臋 zw艂aszcza na wasz膮 pomoc. Pozdrawiam Zuza  |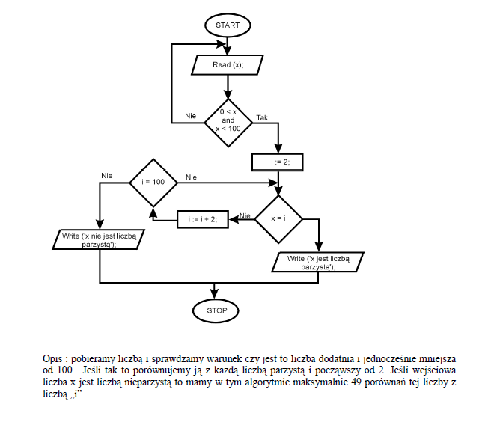
tumor post贸w: 8070 | 2013-11-11 13:53:03 W algorytmie $x$ jest wczytan膮 liczb膮 (szybko sprawdza si臋, czy jest liczb膮 wi臋ksz膮 od $0$, ale mniejsz膮 ni偶 $100$). $i$ przyjmuje na pocz膮tku warto艣膰 $2$. Teraz p臋tla. Sprawdzamy, czy $i=x$. Je艣li teraz (lub p贸藕niej) odpowied藕 jest twierdz膮ca, to wnioskujemy, 偶e $x$ jest parzysty (bo $2$ parzyste, prawda?). Je艣li natomiast odpowied藕 jest przecz膮ca, to zwi臋kszamy $i$ o $2$. Liczba $i$ jest zawsze parzysta. Je艣li $i$ wci膮偶 nie jest r贸wna liczbie $x$, to przyjmuje warto艣ci $4$, potem $6$, potem $8$ itd. Za ka偶dym razem sprawdza si臋, czy $i=x$ (a twierdz膮ca odpowied藕 oznacza, 偶e $x$ parzysty i ko艅czy to program). Gdy $x$ nie jest liczb膮 parzyst膮, to sprawdzimy $i=2,4,6,8,...,96,98$, (a zawsze $x$ nie b臋dzie r贸wny $i$, bo $i$ to tylko liczby parzyste). W贸wczas kolejny raz dodamy do $i$ liczb臋 $2$. Czyli $i=100$. Wiemy natomiast z wcze艣niejszego sprawdzenia, 偶e $x<100$, dlatego liczb parzystych $i$ r贸wnych $100$ lub wi臋kszych ni偶 $100$ nie ma ju偶 sensu sprawdza膰, zatem mo偶na wyj艣膰 z programu z odpowiedzi膮, 偶e $x$ jest nieparzysty. |
zuzannaruda post贸w: 4 | 2013-11-11 14:03:44 wydaje mi si臋, a mo偶e tylko mi si臋 wydaje, 偶e i=100 nie 艣wiadczy o tym 偶e x jest liczb膮 nieparzyst膮 |
zuzannaruda post贸w: 4 | 2013-11-11 14:06:40 ale troch臋 mi to przejasni艂o, w ka偶dym razie dzi臋ki za odpowied藕 |
tumor post贸w: 8070 | 2013-11-11 14:15:00 Je艣li $x$ nie jest liczb膮 parzyst膮, to por贸wnanie go z liczbami $2,4,6,...,96,98$ da wynik negatywny, a zmienna $i$ osi膮gnie warto艣膰 $100$. Je艣li $x$ jest liczb膮 parzyst膮 wi臋ksz膮 od $0$ i mniejsz膮 od $100$, to zmienna $i$ b臋dzie R脫WNA $x$ ZANIM osi膮gnie warto艣膰 $100$. Zatem osi膮gni臋cie przez $i$ warto艣ci $100 $ 艣wiadczy, 偶e $x$ nie by艂 liczb膮 parzyst膮 (cho膰 by艂 liczb膮 wi臋ksz膮 od $0$ i mniejsz膮 od $100$). M贸g艂 by膰 liczb膮 nieparzyst膮, ale m贸g艂 te偶 by膰 liczb膮 nieca艂kowit膮 (bo w programie si臋 w zasadzie nie sprawdza, czy $x$ ca艂kowity) |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj