Liczby rzeczywiste, zadanie nr 4841
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
smog post贸w: 9 |  2014-12-28 16:29:14Bardzo prosz臋 o pomoc w rozwi膮zaniu zada艅. Z g贸ry Bardzo Dzi臋kuje. 1) Wyznacz W(x) + P(x), W(x) − P(x) oraz W(x) $\cdot$ P(x), je艣li: a) W(x) = $3x^{5}$ − $4x^{3}$ +5 , P(x)=−7 b) W(x) = − $x^{4}$ − $2x^{3}$, P(x) = $x^{3}$ −4x 2) Kt贸re z liczb nale偶膮cych do zbioru {−4, −√2 , −1, 1, √2 , 3 } s膮 pierwiastkami wielomianu W(x) = $x^{4}$ − $3x^{2}$ + 2 3) Sprawd藕, czy funkcje okre艣lone wzorami s膮 funkcjami homograficznymi : a) F(x) = $\frac{4x+8}{x+2}$ b) G(x) = $\frac{3x-6}{2}$ 4) Narysuj wykres funkcji a) y= $3x^{2}$ b) y= −$\frac{1}{3}$ $x^{2}$ c) y= $x^{2}$ − 3x+4 5) Rozwi膮偶 r贸wnanie: a) $3x^{4}$ + $3x^{2}$ − 6 = 0 b) $x^{2}$ − 3x − 7 = 0 c) $x^{2}$ − 11x+28 = 0 |
abcdefgh post贸w: 1255 | 2014-12-28 17:18:40 3) $F(x)=\frac{4x+8}{x+2}$ $4\cdot 2 \neq 8*\cdot 1$ $8 \neq 8$ to nie jest funkcja homograficzna b) $G(x)=\frac{3x-6}{2}$ $3\cdot 2=-6 \cdot 0$ to nie jest funkcja homograficzna |
smog post贸w: 9 | 2014-12-28 18:44:12 Dzi臋kuje za pomoc. Zadania 藕le sie zapisa艂y. Tu mam ich odpowiednik na zdj臋ciu. Dzi臋kuje za wszelk膮 pomoc.  |
smog post贸w: 9 | 2014-12-28 18:48:10 Przepraszam za b艂膮d w 6 zadaniu ma by膰 +5 ale nie w pot臋dze  |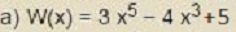
Rafa艂 post贸w: 407 | 2014-12-28 19:03:16 6. a) $W(x)= 3x^{5}-4x^{3}+5 $ $P(x)=-7$ $W(x)+P(x)=3x^{5}-4x^{3}+5 -7= 3x^{5}-4x^{3}-2$ $W(x)-P(x)=3x^{5}-4x^{3}+5 -(-7)= 3x^{5}-4x^{3}+12$ $W(x)*P(x)=3x^{5}-4x^{3}+5 *(-7)= -21x^{5}+28x^{3}-35$ b) $W(x)= -x^{4}-2x^{3} $ $P(x)=x^{3}-4x$ $W(x)+P(x)=-x^{4}-2x^{3}+x^{3}-4x=-x^{4}-x^{3}-4x$ $W(x)-P(x)=-x^{4}-2x^{3}-(x^{3}-4x)=-x^{4}-3x^{3}+4x$ $W(x)*P(x)=(-x^{4}-2x^{3})*(x^{3}-4x)=-x^{7}+4x^{5}-2x^{6}+8x^{4}$ |
Rafa艂 post贸w: 407 | 2014-12-28 19:17:56 9. a)(klik) b)(klik) c)(klik) |
Rafa艂 post贸w: 407 | 2014-12-28 19:29:36 10. a) $3x^{4}+3x^{2}-6=0$ $3x^{4}-3x^{2}+6x^{2}-6=0$ $3x^{2}(x^{2}-1)+6(x^{2}-1)=0$ $(x^{2}-1)(3x^{2}+6)=0$ $(x^{2}-1)=0$ lub $(3x^{2}+6)=0$ $x^{2}=1$ lub $3x^{2}=-6$ $x=1$ lub $x=-1$ drugie r贸wnanie jest sprzecznie, nie posiada rozwi膮zania |
Rafa艂 post贸w: 407 | 2014-12-28 19:35:32 10. b) $x^{2}-3x-7=0$ delta: $9-4*1*(-7)=37$ $x_{1}=\frac{3-\sqrt{37}}{2}$ $x_{2}=\frac{3+\sqrt{37}}{2}$ c) $x^{2}-11x+28=0$ delta: $121-4*1*28=121-112=9$ $x_{1}=\frac{11-\sqrt{9}}{2}=4$ $x_{2}=\frac{11+\sqrt{9}}{2}=7$ PS. W zadaniu 7 nie ma przypadkiem b艂臋du? 呕adna z tych liczb nie jest pierwiastkiem tego wielomianu. Wiadomo艣膰 by艂a modyfikowana 2014-12-28 19:41:07 przez Rafa艂 |
smog post贸w: 9 | 2014-12-28 20:45:50 Bardzo Panu Dzi臋kuje za Pomoc. Jestem dozgonnie wdzi臋czny. Je艣li chodzi o 7 to chyba nie ma 偶adnego b艂臋du. Takie dosta艂em Kt贸re z liczb nale偶膮cych do zbioru {-4, -$\sqrt{2}$, -1, 1, $\sqrt{2}$, 3} s膮 pierwiastkami wielomianu W(x)=$x^{4}$-$3x^{2}$+2 ? Napisa艂em jeszcze raz aby mie膰 pewno艣膰 偶e dobrze. |
Rafa艂 post贸w: 407 | 2014-12-28 21:12:09 Tak jak przypuszcza艂em, na zdj臋ciu jest $2^{2}$, co mnie zmyli艂o. Pierwiastkami tego wielomianu s膮 zatem: $-\sqrt{2}, -1, 1, \sqrt{2} $. |
| strony: 1 2 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj