Inne, zadanie nr 4842
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
lawendka post贸w: 5 |  2014-12-28 19:02:10Witam! Oto zestawy zada艅 jakie dosta艂am do rozwi膮zania.Bardzo prosz臋 o pomoc. Od tego zale偶na jest moja ocena semestralna. Zad. 1. Narysuj wykres funkcji f(x)=3x + $\frac{1}{2}$i wyznacz jej miejsce zerowe. Zad. 2. Dla jakich warto艣ci b miejscem zerowym funkcji f(x)= -4+2b+1 jest liczba mniejsza od 4? Zad.3. Wska偶 r贸wnanie prostej, kt贸ra nie jest r贸wnoleg艂a do prostej y=$\sqrt{3x}$: A. y=$\frac{3}{\sqrt{3}}$ x B. y= (1 + $\sqrt{3}$ )x C. y= -2 + $\sqrt{3x}$ D. y= $\frac{\sqrt{27}}{3}$x - $\sqrt{3}$ Zad.4. Zapisz r贸wnanie prostej w postaci kierunkowej: a) 5x-6y=0 b) 2x+3y-6=0 c) - $\sqrt{8y}$+ $\sqrt{2}$= 0 Zad.5. Wska偶 sprzeczny uk艂ad r贸wna艅 A.$\left\{\begin{matrix} x+2=0 \\ y-3=0 \end{matrix}\right.$ B. $\left\{\begin{matrix} 5x-7y=0 \\ 7x-5y=2 \end{matrix}\right.$ C. $\left\{\begin{matrix} \sqrt{2x}-y=\sqrt{8} \\ -2x+ \sqrt{2y}-4=0 \end{matrix}\right.$ D. $\left\{\begin{matrix} x+y=3 \\ 3x+3y-9=0 \end{matrix}\right.$ Zad.6. Wska偶 posta膰 og贸ln膮 funkcji kwadratowej f(x)=2$(x-3)^{2}$-7 : A. f(x)=$2x^{2}$+ 11 B. f(x)=$2x^{2}$-6x+11 C. f(x)=$2x^{2}$-12x+11 D. f(x)=$2x^{2}$-12x+2 Zad.7. Wska偶 zbi贸r wszystkich rozwi膮za艅 nier贸wno艣ci 16x-$4x^{2}$$\le$0 A. (-$\infty$;-4)$\cup$(0;$\infty$) B. (0;4) C. (-$\infty$;0)$\cup$(4;$\infty$) D. (4;$\infty$) |
abcdefgh post贸w: 1255 | 2014-12-28 19:35:38 zad.1 $f(x)=3x+\frac{1}{2}$ $3x=-\frac{1}{2}$ $x=\frac{-1}{6}$ 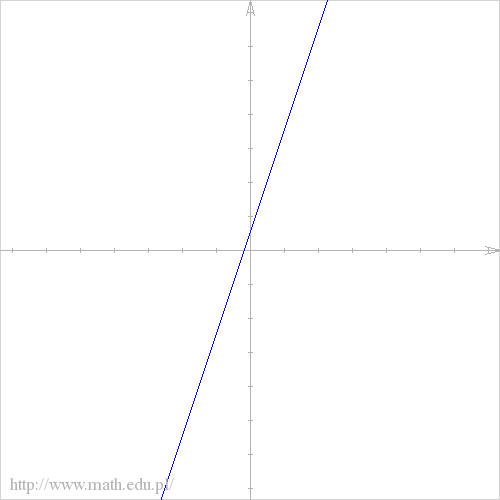 zad.3 $y=\sqrt{3}x$ $a_{1}=a_{2}$ C.y=$-2+\sqrt{3}x$ zad.4 a) 5x-6y=0 $6y=5x \ \ \ \ \ \ y=\frac{5}{6}x$ b) 2x+3y-6=0 $3y=6-2x \ \ \ \ \ y=2-\frac{2}{3}x$ c) $sqrt{8y}=\sqrt{2}$ $8y=2$ $y=\frac{1}{4}$ zad.5 C. $\left\{\begin{matrix} \sqrt{2x}-y=\sqrt{8} |\cdot \sqrt{2} \\ -2x+ \sqrt{2y}-4=0 \end{matrix}\right.$ $\left\{\begin{matrix} 2x-\sqrt{2x}y=4 \\ -2x+ \sqrt{2y}-4=0 \end{matrix}\right.$ $0=8$ zad.6 $f(x)=2(x-3)^{2}-7=2(x^2-6x+9)-7=2x^2-12x+18-7=2x^2-12x+11$ zad.7 $16x-4x^2 \le 0$ $4x(4-x) \le 0$ x=0 x=4 $x \in (-\infty,0] \cup [4,+\infty)$ |
lawendka post贸w: 5 | 2015-01-06 18:47:03 Dzi臋kuj臋 bardzo! |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj