Stereometria, zadanie nr 4912
ostatnie wiadomości | regulamin | latex
| Autor | Zadanie / Rozwiązanie |
| ziemniak postów: 6 |  2015-01-18 13:58:09Dany jest ostrosłup prawidłowy sześciokątny. Krawędź boczna ostrosłupa jest dwa razy dłuższa od krawędzi jego podstawy. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa. |
| abcdefgh postów: 1255 | 2015-01-18 16:20:22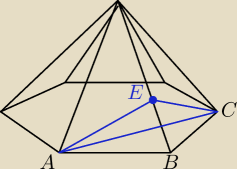 $k_{b}=2k_{p}$ $AC= \sqrt{3}k_{p}$ $\angle|AEC| =cos \alpha $ trzeba skorzytsać z tw. cosinusów h-wysokość ściany bocznej $h^2+ (\frac{k_{p}}{2})^2=(2k_{p})^2$ $h=\frac{k_{p}\sqrt{15}}{2}$ Obliczmy AE: $\frac{1}{2}k_{p}\frac{k_{p}\sqrt{15}}{2}=\frac{1}{2} 2k_{p}*|AE| $ $|AE|=\frac{k_{p}\sqrt{15}}{4}$ i podstawić do tw. cosinusów: $|AC|^2=|AE|^2+|EC|^2-2|AE||EC| cos\alpha$ gdzie |EC|=|AE| |
| strony: 1 | |
Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj