Planimetria, zadanie nr 55
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
steeve post贸w: 5 |  2010-04-01 21:10:16Zad. W tr贸jk膮t r贸wnoboczny o boku \"a\" cm wpisano kwadrat. Oblicz pole tego kwadratu. Pr贸bowa艂em to oblicza膰 z trygonometri, bior膮c pod uwag臋, 偶e ka偶dy k膮t ma 60 stopni, nie da艂o rady: / |
Mariusz 艢liwi艅ski post贸w: 489 | 2010-04-01 22:17:37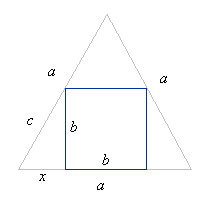 Wprowad藕my oznaczenia jak na rysunku. Tr贸jk膮t o bokach x, b, c jest prostok膮tny. D艂ugo艣膰 boku c jest dwukrotnie wi臋ksza od d艂ugo艣ci boku x. $c = 2x$ Z tw. Pitagorasa $b^2 = c^2 - x^2$ $b^2 = (2x)^2 - x^2$ $b^2 = 3x^2 \Rightarrow x = \frac{\sqrt{3}}{3}b$ $a = 2x + b = 2 \cdot \frac{\sqrt{3}}{3}b + b$ $3a = 2\sqrt{3}b + 3b$ $b(2\sqrt{3}+3) = 3a$ $b = \frac{3a}{2\sqrt{3}+3} $ Pozbywamy si臋 niewymierno艣ci z mianownika $b = \frac{3a}{2\sqrt{3}+3} \cdot \frac{2\sqrt{3}-3}{2\sqrt{3}-3} = \frac{6a\sqrt{3}- 9a}{3} = 2a\sqrt{3}- 3a = a(2\sqrt{3} - 3)$ Pole kwadratu: $P = b^2$ $P = {(a(2\sqrt{3} - 3))}^2$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj