Liczby rzeczywiste, zadanie nr 5590
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
chomik7967 post贸w: 21 |  2015-12-11 15:24:37Rozwi膮偶 uk艂ad r贸wna艅: $x+y=10$ $x^3+x^3y^3+y^3=800$ Pr贸bowa艂em w ten spos贸b: zapisa艂em drugie r贸wnanie jako: $(x+y)(x^2-xy+y^2)+x^3y^3=800$ $10(x^2-xy+y^2)+x^3y^3=800$ $10[(x+y)^2-3xy]+x^3y^3=800$ $10(x+y)^2-30xy+x^3y^3=800$ $10(10)^2-30xy+x^3y^3=800$ $1000-30xy+x^3y^3=800$ $x^3y^3-30xy=-200$ $xy(x^2y^2-30)=-200$ Nie bardzo wiem co dalej zrobi膰 i czy dobrze rozumuj臋 :) Wiadomo艣膰 by艂a modyfikowana 2015-12-11 15:26:44 przez chomik7967 |
magda95 post贸w: 120 | 2015-12-11 18:49:00 W ostatnim r贸wnaniu mo偶esz podstawi膰 $y = 10 - x $. Dostaniesz r贸wnanie czwartego stopnia, ale to powinno da膰 si臋 rozwi膮za膰. Ew. mo偶na by艂o od razu podstawi膰 $y = 10 - x$, ale r贸wnanie z $x^6$ by艂oby bardzo nieprzyjemne Wiadomo艣膰 by艂a modyfikowana 2015-12-11 18:49:43 przez magda95 |
chomik7967 post贸w: 21 | 2015-12-19 20:57:12 Nadal nie mog臋 rozwi膮za膰 tego uk艂adu, sporo nad nim my艣l臋 jak mam czas i spr贸bowa艂em troch臋 inaczej to zrobi膰 ale wci膮偶 nie mog臋 go rozwi膮za膰 :( $x+y=10$ $x^3+x^3*y^3+y^3=800$ Drugie r贸wnanie zapisa艂em tym razem w ten spos贸b: $x^3y^3+y^3=800-x^3$ $y^3(x^3+1)=800-x^3$ Nast臋pnie podstawiam y=10-x $(10-x)^3(x^3+1)=800-x^3$ Po uproszczeniu wychodzi wielomian stopnia 6... :( przerasta mnie troch臋 ten uk艂ad Wpisywa艂em te偶 te r贸wnania w r贸偶ne programy by wiedzie膰 chocia偶 co lub ile mniej wi臋cej powinno wyj艣膰. Rozwi膮zania to przeci臋cia tych wykres贸w  |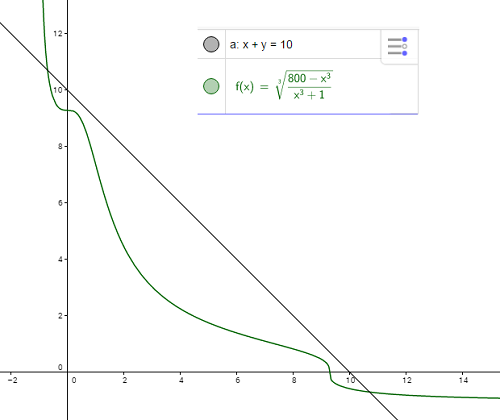
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj