Planimetria, zadanie nr 5809
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
nice1233 post贸w: 147 |  2016-05-27 13:06:20ZAD 3 Styczne do okr臋gu w punktach K, L, M przecinaj膮 si臋 w punktach A, B, C, jak na rysunku obok. Wiadomo, 偶e |AC| = |BC| = 5 oraz obw贸d tr贸jk膮ta ABC jest r贸wny 18. Z tego wynika, 偶e: A. |CL| = 0,5 B. |CL| = 1 C. |CL| = 1,5 D. |CL| = 2 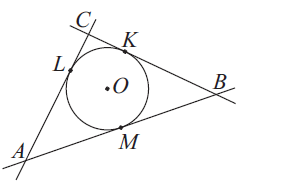 Czy dobrze zrobi艂臋m zadania ? Jak co艣 to napiscie co i jak mam 藕le lub jakom艣 wskaz贸wk臋. Dzi臋ki :) Moje rozwi膮zanie: https://3.bp.blogspot.com/-x3_Q2aIMnSI/V0glvmBMjnI/AAAAAAAACzo/Yw-JT2noz50TasTtxqfcZVRq8l5Ad_RPgCLcB/s1600/Zdj%25C4%2599cie-0018.jpg |
sylwia94z post贸w: 134 | 2016-05-27 19:15:17 Masz b艂膮d bo napisa艂e艣 w tym uk艂adzie 16 zamiast 18. A tak to spos贸b dobry. Prawid艂owa odpowied藕 B. |
janusz78 post贸w: 820 | 2016-05-27 19:36:57 Z twierdzenia o d艂ugo艣ci odcink贸w stycznych poprowadzonych z danego punktu do okr臋gu: $ |AL|=|AM|=y, \ \ |CL|=|CK|=x, \ \ |BM|=|BK|= z.$ Z tre艣ci zadania: $|AC|=|BC|=5,$ czyli $x+y = x+z =5,$ (1) oraz $|AC|+|BC|+|CA| = 18,$ czyli $2x+2y +2z =18, \ \ x + y + z = 9.$ (2) Z uk艂adu r贸wna艅 (1), (2): $ x = 1, \ \ y=4, \ \ z= 4.$ $|CL|= x =1.$ Odpowied藕: B. |
nice1233 post贸w: 147 | 2016-05-27 21:35:56 Dzi臋kuje :) |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj