Planimetria, zadanie nr 5815
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
nice1233 post贸w: 147 |  2016-05-28 13:11:08Obilcz $\alpha\beta\gamma$  |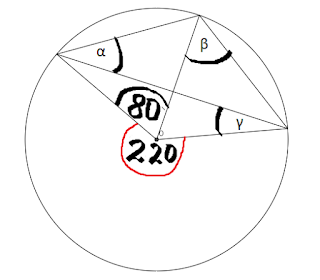
janusz78 post贸w: 820 | 2016-05-28 16:09:57 $ 2\gamma +80^{o}+60^{o}= 180^{o} $ - suma miar k膮t贸w w tr贸jk膮cie (tr贸jk膮t r贸wnoramienny). $ \gamma = 20^{o}.$ $ 2\alpha = 60^{o}$ miara k膮ta wpisanego opartego na 艂uku tym samym co k膮t 艣rodkowy o mierze $60^{o}.$ $\alpha = 30^{o}.$ $ \delta + \beta = 110^{o}$ miara k膮ta wpisanego opartego na 艂uku tym samym co k膮t 艣rodkowy o mierze $220^{o} $ (*) $80^{o}+\gamma +\alpha +\delta = 180^{o}$ - suma miar k膮t贸w w tr贸jk膮cie. Z ostatniego r贸wnania, po uwzgl臋dnieniu warto艣ci miar k膮t贸w $\alpha, \ \ \gamma$ $ \delta = 50^{o}$ Z r贸wnania (*) $\beta = 110^{o}-50^{o}=60^{o}.$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj