Logika, zadanie nr 1558
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
kaktusx22 post贸w: 3 |  2013-10-04 20:39:43Cze艣膰 , czy kto艣 mo偶e pom贸c z zadaniami http://oi40.tinypic.com/v63goi.jpg 10, 9 , 8 , 5 |
abcdefgh post贸w: 1255 | 2013-10-05 00:24:53 zad.9 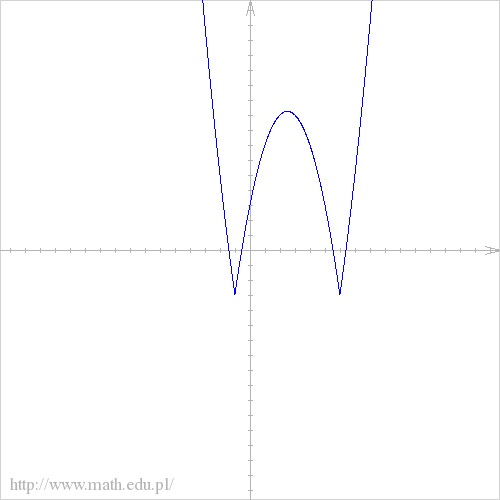 $D=R$ $ZW= <-3,+\infty)$ Zad.5 $A={x : |x-1|+|x+1|=2} A = <-1,1>$ $B={x: \frac{1}{x-5}+\frac{3}{x+3}-\frac{4}{x} \ge 0}$ $B= x \in (-3,0) \ \cup \ (5,15> $ $C={x: \sqrt{x^2+4}<2-x}$ $C = x<0 $ $D={x: \frac{1}{8}*4^{2x-3}>\frac{\sqrt{2}}{8}}^{-x}$ $D= x>6$ $A\'=R\(-1,1)$ $A\'\cap B=(-3,-1)\cup (5,15)$ $C \B=(-\infty,-3>$ $A\cup B\cup C\cup D=(-\infty,1> \cup (5,+\infty)$ |
abcdefgh post贸w: 1255 | 2013-10-05 01:28:49 zad.10 a) $f(x)=x^2+4x+3 \ g(x)=\sqrt{x+1}$ $D_{f}=R \ ZW_{f}=<-1,+\infty$ $D_{g}=<-1;+\infty) \ ZW_{g}=<0,+\infty)$ $Z艂o偶enie \ funkcji \ istnieje \ gdy偶$ $ZW_{g} \in D_{f}$ $g \circ f =\sqrt{x^2+4x+4}=x+2$ $b)f(x)=\frac{2x+3}{x+1} \ g(x)=\frac{1}{|x-2|}$ $D_{f}=R\{-1} \ ZW_{f}=R\{2}$ $D_{g}=R\{2} \ ZW_{g}=(0,+\infty)$ $g \circ f=\frac{1}{|\frac{2x+3}{x+1}-2|}=\frac{1}{|\frac{2x+3-2x-2}{x+1}|}=\frac{1}{1}=1$ c) f(x)=sgn(x-1) g(x)=$x^2-2x-2$ $D_{f}=R \ \ ZW_{f}=<-1,1>$ $D_{g}=R \ \ ZW_{g}=<-3,+\infty)$ $g \circ f =(sgn(x-1))^2-2(sgn(x-1))-2$ |
abcdefgh post贸w: 1255 | 2013-10-05 01:44:42 zad.8 A= $3^{|x|+2} \ge 3^3$ $|x| \ge 1$ $x \in (-\infty;-1> \cup <1,\infty)$ $y(y^2+5y-6) \le 0$ $y(y+6)(y-1) \le 0$ $y \in <-6,0> \cup <1,+\infty)$  |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj