Algebra, zadanie nr 1799
ostatnie wiadomości | regulamin | latex
| Autor | Zadanie / RozwiÄ…zanie |
justa_tj2 postów: 1 |  2013-12-10 11:20:32Zbadaj przebieg zmienności funkcji 3x^{2} - 4 + \frac{1}{x} 3 x kwadrat - 4 + 1 przez x |
abcdefgh postów: 1255 | 2013-12-22 16:03:17 $f(x)=3x^2-4+\frac{1}{x}=\frac{3x^3-4x+1}{x}$ $D_{f}=R$\{$0$} asymptoty poziome: $lim_{x \to 0^{+} }(\frac{3x^3-4x+1}{x})=lim_{x \to 0^{+} }(\frac{3x^2-4+\frac{1}{x}}{1})=+\infty$ $lim_{x \to 0^{-} }(\frac{3x^3-4x+1}{x})=lim_{x \to 0^{-} }(\frac{3x^2-4+\frac{1}{x}}{1})=-\infty$ asymptota pozioma jest w punkcie $x_{o}=0$ asymptota ukośna: $lim_{x \to \infty }\frac{f(x)}{x}=lim_{x \to \infty }\frac{3x^3-4x+1}{x^2}=lim_{x \to \infty }\frac{3x-\frac{4}{x}+\frac{1}{x^2}}{1}=\infty$ $lim_{x \to -\infty }\frac{f(x)}{x}=-\infty$ nie ma asymptot ukośnych (też pionowych) monotoniczność,esktrema $f\'(x)=6x-\frac{1}{x^2}=\frac{6x^3-1}{x^2}$ $D_{f}=R$\{0} $\frac{6x^3-1}{x^2}=0$ $x=\frac{1}{\sqrt[3]{6}}$ 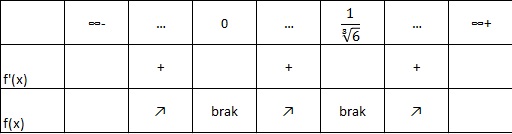 $f\"(x)=6+\frac{2}{x^3}=\frac{6x^3+2}{x^3}$ $D_{f}=R$\{0} $\frac{6x^3+2}{x^3}=0$ $x=\frac{-1}{\sqrt[3]{3}}$  |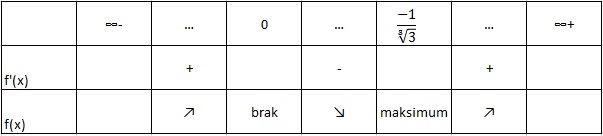
abcdefgh postów: 1255 | 2013-12-22 16:04:07 parzystość: $f(-x)=\frac{-3x^3+4x+1}{-x}$ nieparzysta |
| strony: 1 | |
Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj