Inne, zadanie nr 2923
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
dora1606 post贸w: 29 |  2014-12-20 22:08:08Bardzo prosz臋 o pomoc z wyt艂umaczeniem krok po kroku:) \lim_{x \to \infty}8log2_{n\div}2^{n} |
dora1606 post贸w: 29 | 2014-12-20 22:11:23 |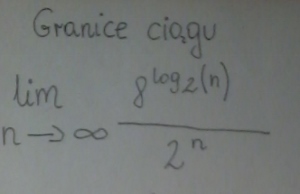
abcdefgh post贸w: 1255 | 2014-12-20 22:15:22 $\lim_{n \to \infty} \frac{8^{log_{2}n}}{2^n}=\lim_{n \to \infty} \frac{n^3}{2^n}=0$ |
dora1606 post贸w: 29 | 2014-12-20 22:21:31 a mog臋 wiedzie膰 dok艂adnie sk膮d si臋 wzi臋艂o to n3 itd? |
tumor post贸w: 8070 | 2014-12-21 02:18:16 wzi臋艂o si臋 z liceum. Niekt贸rzy ludzie przed studiami odwiedzaj膮 liceum. By艂 wz贸r $a^{log_ab}=b$, st膮d $2^{log_2n}=n$ czyli $8^{log_2n}=(2^{3})^{log_2n}=(2^{log_2n})^3=n^3$ Je艣li chodzi o granic臋, to wynika na przyk艂ad z regu艂y de l\'Hospitala, ale mo偶na to zrobi膰 na zwyk艂e przemy艣lenie. Mo偶na dla przyk艂adu dowie艣膰 indukcyjnie, 偶e dla pewnego $n_0$ i $n>n_0$ mamy $2^n>n^4$. We藕my $n_0=100$, wtedy $(n_0)^4=10^8$, natomiast $2^{n_0}>10^30$. (bo $2^{10}>10^3$). Je艣li ponadto $2^n>n^4$, to $2^{n+1}=2*2n>2n^4>n^4+ 99n^3>n^4+4n^3+6n^2+4n+1=(n+1)^4$ A skoro dla $n>n_0$ mamy $2^n>n^4$, to tak偶e $0<\frac{n^3}{2^n}<\frac{1}{n}$ i z twierdzenia o trzech ci膮gach, skoro $0\to 0$ i $\frac{1}{n}\to 0$, to tak偶e ci膮g z zadania ma granic臋 0 |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj