Inne, zadanie nr 3475
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
magdalena132 post贸w: 18 |  2015-06-02 14:37:36[img]http:// 11264847_10200291952579159_2514239272614787836_n |
magdalena132 post贸w: 18 | 2015-06-02 15:07:35 |
magdalena132 post贸w: 18 | 2015-06-02 15:09:09 |
magdalena132 post贸w: 18 | 2015-06-02 15:10:50 |
magdalena132 post贸w: 18 | 2015-06-02 15:11:13 |
magdalena132 post贸w: 18 | 2015-06-02 15:11:40 |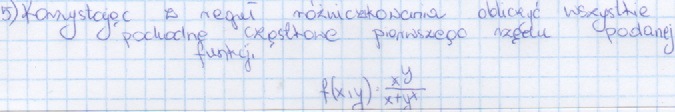
janusz78 post贸w: 820 | 2015-06-02 16:37:46 Zadanie 1 a) $\int (3+5x)^8dx $ $3 +5x =t, 5dx =dt, dx=\frac{1}{5}dt$ $\frac{1}{5}\int tdt = \frac{1}{5}(3x+5)+C.$ b) $\int(x\sqrt{1+x^2}dx$ $\sqrt{1+x^2}=t, 1+x^2=t^2, 2xdx=2tdt, xdx=tdt,$ $\int t^2dt = \frac{t^3}{3}+C= \frac{1}{3}(\sqrt{1+x^2})^3+ C.$ c) $\int\cos(2x)dx $ $2x =u, 2dx =du, dx=\frac{1}{2}u.$ $\frac{1}{2}\int cos(u)du = \frac{1}{2}\sin(u)+C= \frac{1}{2}sin(2x)+C.$ Zadanie 4 - patrz rozwi膮zanie Forum Zadanie 5 $\int_{-\infty}^{0}\frac{1}{e^{4x}}dx = \int_{-\infty}^{0}e^{-4x}dx= -\frac{1}{4}e^{-4x}|_{x\rightarrow -\infty}^{0}= -\frac{1}{4}+ \infty = \infty.$ Ca艂ka rozbie偶na do $\infty.$ Zadanie 6 $f\'_{|x}(x,y)= \frac{yx^{y-1}-x^{y}\cdot 1}{(x+y^{x})^2}.$ $f\'_{|y}(x,y)= \frac{x^{y}\ln(x)(x+y^{x})-x^{y}\cdot xy^{x-1}}{(x+y^{x})^2}.$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj