Analiza matematyczna, zadanie nr 3986
ostatnie wiadomości | regulamin | latex
| Autor | Zadanie / RozwiÄ…zanie |
benq7594 postów: 3 |  2015-12-13 17:53:59Witam, muszę zbadać zbieżność trzech szeregó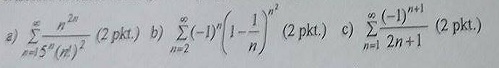w.  W pierwszym szeregu, za pomocą kryterium D\'Alamberta wyszło mi $\frac{\epsilon^2}{5}$ czyli >1 czyli szereg rozbieżny. W drugim szeregu, najpierw wstawiłem wartość bezwzględną, potem za pomocą kryterium Cauchy\'ego, wyszła mi liczba $\epsilon$ czyli rozbieżny, następnie sprawdziłem warunki, zgadzały się czyli szereg zbieżny warunkowo za pomocą kryterium Leibnitz\'a. W trzecim szeregu, wartość bezwzględna, kryterium porównawcze, wyszło $\frac{1}{2} * \frac{1}{n}$ czyli rozbieżny szereg harmoniczny, i dalej warunkowo zbieżny przez kryterium Leibnitz\'a. Czy ktoś mógłby sprawdzić czy zrobiłem to dobrze ? Przepraszam, że nie wrzucam obliczeń pośrednich, ale nigdy nie korzystałem z takiego forum i bardzo długo zajęłoby mi wpisywanie tego za pomocą tych symboli, z góry bardzo dziękuję za odpowiedź. |
janusz78 postów: 820 | 2015-12-13 21:37:06 Pierwszy szereg - bezbłędnie. Drugi- kryterium Leibniza, nie Cauchy, bo szereg naprzemienny. i ciąg $( 0 < a_{n}= (1-1/n)^{n^2}) $-zbieżny do $ 0 $ - szereg zbieżny Trzeci na podstawie kryterium Leibniza, bo szereg naprzemienny, ciąg $ 0< a_{n}= \frac{1}{2n+1}$ malejący, zbieżny do zera - szereg zbieżny. Wiadomość była modyfikowana 2015-12-13 22:16:16 przez janusz78 |
tumor postów: 8070 | 2015-12-14 09:03:29 Nie myl ludzi, Janusz. Drugi szereg Cauchy, a nie Leibniz. Leibniz nie daje informacji, czy zbieżność nie jest tylko warunkowa, a Cauchy zastosowany do szeregu wartości bezwzględnych daje zbieżność bezwzględną, stąd i szereg b) jest zbieżny bezwzględnie, ponieważ $\lim_{n \to \infty}(1-\frac{1}{n})^n=e^{-1}<1$ |
| strony: 1 | |
Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj