Rachunek róşniczkowy i caĹkowy, zadanie nr 4168
ostatnie wiadomoĹci | regulamin | latex
| Autor | Zadanie / RozwiÄ zanie |
elcia199210 postĂłw: 1 |  2016-01-23 21:11:49 2016-01-23 21:11:49CaĹki to moja sĹaboĹÄ nigdy ich nie zrozumiem a mam do zrobienia 3 zadania na zaliczenie. ByĹabym bardzo wdziÄczna za pomoc. 1. Oblicz pole obszaru ograniczonego krzywÄ y=x^{2}-4 a osiÄ Ox na przedziale [-3,2]. 2. Niech bÄdzie dana prosta przechodzÄ ca przez punkty (-1,1) oraz (3,9)na przedziale [0.2]. a) Oblicz pole ograniczone odcinkiem prostej a osiÄ Ox b) Oblicz objÄtoĹÄ bryĹy powstaĹej z obrotu odcinka prostej do okoĹa osi Ox. c) oblicz pole powierzchni caĹkowitej powstaĹej bryĹy d) oblicz dĹugoĹÄ odcinka prostej 3. RozwiÄ Ĺź rĂłwnanie róşniczkowe. Wyniki pozostawiÄ w postaci jawnej. a) xyy\"=(4x^{2}-3)/y=0 B)xyy\"=(x+3)/(9x^{2}+6x+17 |
janusz78 postĂłw: 820 |  2016-01-24 13:46:42 2016-01-24 13:46:421. Rysunek $|P|= \int_{-3}^{-2} (x^2-4)dx +\int_{-2}^2(-x^2+4)dx=...$ 2. Rysunek RĂłwnanie prostej $ y = \frac{9-1}{3+1}(x+1)+1= 2x+3, \ \ x\in(0, 2).$ a) $\int_{0}^{2}(2x+3)dx=...$ b) ObjÄtoĹÄ stoĹźka ĹciÄtego $|V|= \pi\int_{0}^{2}(2x+3)^2dx =...$ Ze wzoru szkolnego na objÄtoĹÄ stoĹźka ĹciÄtego $|V|= \frac{1}{3}\pi\cdot 2(3^2+ 3\cdot 7 + 7^2).$ c) Pole powierzchni caĹkowitej stoĹźka ĹciÄtego $|S|= \pi\cdot 3^2 + 2\pi \int_{0}^{2}(2x+3)\sqrt{1+2^2}dx + \pi\cdot 7^2=...$ Ze wzoru szkolnego na pole powierzchni caĹkowitej stoĹźka ĹciÄtego: $|S| = \pi(3^2+7^2)+\pi(3+7)\sqrt{(7-3)^2+2^2}.$ d) DĹugoĹÄ odcinka prostej $|AB|= \int_{0}^{2}\sqrt{1+2^2}dx=...$ Zadanie 3 w postaci bardziej czytelnej, proszÄ umieĹciÄ w oddzielnym poĹcie. WiadomoĹÄ byĹa modyfikowana 2016-01-24 13:56:53 przez janusz78 |
kadia postów: 11 |  2016-01-24 17:41:39 2016-01-24 17:41:39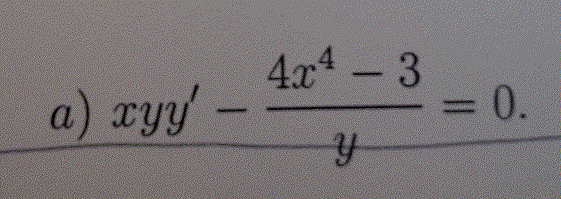 bardziej czytelna róşniczka 1 bardziej czytelna róşniczka 1 |
kadia postĂłw: 11 |  2016-01-24 17:43:58 2016-01-24 17:43:58 bardziej czytelna róşniczka 2 (bardzo proszÄ o pomoc bardziej czytelna róşniczka 2 (bardzo proszÄ o pomoc |
kadia postĂłw: 11 |  2016-01-24 18:01:44 2016-01-24 18:01:44To sÄ róşniczki koleĹźanki elcia199210 , rĂłwnieĹź proszÄ o pomoc |
janusz78 postĂłw: 820 |  2016-01-24 19:37:38 2016-01-24 19:37:38ProszÄ zapoznaÄ siÄ z regulaminem forum. a) Rozdzielamy zmienne. $ y^2dy = \frac{4x^4-3}{x}dx.$ CaĹkujemy obustronnie $ \int y^2dy = \int \frac{4x^4-3}{x}dx.$ $\int y^2 dy = \int 4x^3dx -3\int \frac{1}{x}dx$ StÄ d $\frac{1}{3}y^3 = x^4 -3\ln|x| + A $ RozwiÄ zanie ogĂłlne rĂłwnania (caĹka ogĂłlna) $ y = \sqrt[3]{3x^4 -9\ln|x|+ C}, \ \ C= 3A.$ Drugie rĂłwnanie róşniczkowe a) rozwiÄ zujemy identycznie. |
kadia postĂłw: 11 |  2016-01-24 19:51:36 2016-01-24 19:51:36DziÄkujÄ, i przepraszam za zdjÄcia. Przepraszam tam gdzie Pan napisaĹ \" y2dy \" nie powinno byÄ czasami xyy\' ? |
janusz78 postĂłw: 820 |  2016-01-24 20:15:06 2016-01-24 20:15:06Nie, bo rozdzieliliĹmy zmienne $xy \frac{dy}{dx} = \frac{4x^4 -3}{y} |\cdot y$ $ xy^2\frac{dy}{dx}= x^4 -3|:x $ $ y^2 \frac{dy}{dx} = \frac{x^4 -3}{x}|\cdot dx $ $ y^2 dy = \frac{x^4-3}{x}dx, \ \ x\neq 0.$ |
| strony: 1 | |
Prawo do pisania przysĹuguje tylko zalogowanym uĹźytkownikom. Zaloguj siÄ lub zarejestruj