Rachunek róşniczkowy i caĹkowy, zadanie nr 4171
ostatnie wiadomoĹci | regulamin | latex
| Autor | Zadanie / RozwiÄ zanie |
kadia postĂłw: 11 |  2016-01-24 18:13:48 2016-01-24 18:13:48Bardzo potrzebujÄ, pomocy przy rozwiÄ zaniu tych dwĂłch caĹek. Na prawdÄ sama nie potrafiÄ sobie z nimi poradziÄ. ProszÄ o szybkÄ pomoc.. ;( |
kadia postĂłw: 11 |  2016-01-24 18:14:41 2016-01-24 18:14:41jedna z nich 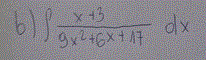 |
kadia postĂłw: 11 |  2016-01-24 18:15:25 2016-01-24 18:15:25druga 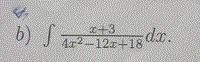 proszÄ o pomoc |
janusz78 postĂłw: 820 |  2016-01-24 19:23:23 2016-01-24 19:23:23Patrz regulamin forum, skany nie sÄ mile widziane! $ \int\frac{x+3}{9x^2+6x +17}dx = \int \frac{x}{9x^2+6x+17}dx +\int\frac{3}{9x^2+6x +17}dx = I_{1}+ I_{2}.$ PierwszÄ z caĹek sprowadzamy do pochodnej z logarytmu naturalnego mnoĹźÄ c licznik i mianownik przez 18 oraz dodajÄ c - i odejmujÄ c 6 (Ĺźeby siÄ nic nie zmieniĹo). A drugÄ z caĹek wraz z caĹkÄ wynikajÄ cÄ z odjÄcia 6, to jest caĹkÄ $ \frac{8}{3}\int \frac{1}{9x^2+6x +17}dx $ sprowadzamy do caĹki z arkusa tangensa, przeksztaĹcajÄ c trĂłjmian kwadratowy $9x^2 +6x +17 $ do postaci kanonicznej. DrugÄ caĹkÄ b) obliczamy w ten sam sposĂłb. WiadomoĹÄ byĹa modyfikowana 2016-01-24 20:23:43 przez janusz78 |
kadia postĂłw: 11 |  2016-01-24 20:15:53 2016-01-24 20:15:53MĂłgĹby Pan obliczyÄ przynajmniej tÄ jednÄ caĹkÄ do koĹca ? Bo nie mam pojÄcia czy to dobrze obliczam. Bardzo proszÄ. |
janusz78 postĂłw: 820 |  2016-01-24 20:24:43 2016-01-24 20:24:43PokaĹź swoje obliczenia ! |
kadia postĂłw: 11 |  2016-01-24 20:34:17 2016-01-24 20:34:17∫x/9x2+6x+17dx + ∫3/9x2+6x+17dx = ∫18x/162+108+306dx +∫1/3x2+2x+17dx= i nie wiem co dalej od tej pierwszej odejmowaÄ 6 ? |
kadia postĂłw: 11 |  2016-01-24 20:35:38 2016-01-24 20:35:38CoĹ mi nie wyszĹo przepisanie, dodam zdjÄcie |
kadia postĂłw: 11 |  2016-01-24 20:40:30 2016-01-24 20:40:30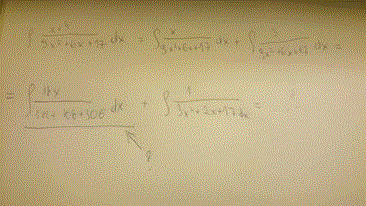 |
janusz78 postĂłw: 820 |  2016-01-24 21:18:10 2016-01-24 21:18:10$I_{1}+I_{2} = \int \frac{x}{9x^2 +6x +17}dx + 3\int\frac{1}{9x^2 +6x +17}dx = \frac{1}{18}\int \frac{18x +6 -6}{9x^2 +6x +17}dx + 3 \int \frac{1}{9x^2 +6x +17}dx,$ $I_{1}+I_{2} = \frac{1}{18}\int \frac{18x +6}{9x^2 +6x +17}dx - \frac{1}{3}\int \frac{1}{9x2 +6x+17}dx +3\int \frac{1}{9x^2+6x+17}dx, $ $I_{1}+I_{2}= \frac{1}{18} \ln(9x^2+6x +17) + A + \frac{8}{3}\int \frac{1}{9x^2 + 6x +17}dx = \frac{1}{18}\ln(9x^2 +6x +17) + A + I_{3},$ $ I_{3}= \frac{8}{3}\int \frac{1}{9x^2 +6x +17}dx.$ Mianownik funkcji podcaĹkowej sprowadzamy do postaci kanonicznej i postaci pochodnej z funkcji arkus tangens. $ 9x^2 +6x +17 = 9\left( x^2 +2\cdot \frac{1}{3}x +(\frac{1}{3})^2 + \frac{16}{9}\right)= 9 [(x+\frac{1}{3})^2+\frac{16}{9}].$ $ 9x^2 +6x +17 = \frac{81}{16}\left[ \frac{(x+\frac{1}{3})^2}{\frac{16}{9}} + 1 \right]= \frac{81}{16}\left[ (\frac{3x+1}{4})^2 +1 \right].$ Podstawienie $ \frac{3x+1}{4} = t, \ \ \frac{3}{4}dx = dt \ \ dx = \frac{4}{3}dt.$ $ I_{3}= \frac{8}{3}\cdot \frac{16}{81}\cdot \frac{4}{3}\int \frac{1}{t^2 +1}dt = \frac{492}{729}\arctan\left(\frac{3x+1}{4}\right) + B.$ $ I_{1}+I_{2}= \frac{1}{18}\ln(9x^2 +6x +17)+\frac{492}{729}\arctan\left(\frac{3x+1}{4}\right) + C, \ \ C = A + B.$ |
| strony: 1 | |
Prawo do pisania przysĹuguje tylko zalogowanym uĹźytkownikom. Zaloguj siÄ lub zarejestruj