logowanie

Matematyka dyskretna, zadanie nr 4496

ostatnie wiadomości  |  regulamin  |  latex

Autor	Zadanie / RozwiÄ zanie
geometria postĂłw: 865	2016-04-25 16:53:20 Podaj jakie wlasnosci (zwrotna, symetryczna, slabo antysymetryczna (($\forall_{x,y}\in X$)$xRy \wedge yRx \Rightarrow x=y $), przechodnia) maja relacje okreslone za pomoca diagramu.
tumor postĂłw: 8070	2016-04-25 17:08:28 Hm, nie brakuje diagramu?
geometria postĂłw: 865	2016-04-25 17:54:39
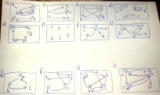geometria postĂłw: 865	2016-04-25 17:55:47 Tylko nic nie widac.
tumor postĂłw: 8070	2016-04-25 18:03:23 No to jak mam powiedzieć? MoĹźesz diagramy opisać. Wypisz wszystkie elementy (punkty), jakie się pojawiajÄ . W diagramie zapewne sÄ strzałki, więc wypisz teĹź strzałki w postaci (poczÄ tek,koniec). Wiadomość była modyfikowana 2016-04-25 18:04:38 przez tumor
geometria postĂłw: 865	2016-04-25 18:13:04 Czyli np. jezeli jest strzalka z punktu a do punktu b, to napisac (a,b), jak z punktu a do punktu a, to (a,a) itd. tak? Jutro to dokoncze.
tumor postów: 8070	2016-04-25 18:15:36 tak. Albo skombinuj lepsze zdjęcie. Natomiast zawsze lepszy jest dla mnie tekst od zdjęcia.
geometria postĂłw: 865	2016-04-26 09:19:44 a) punkty na diagramie: $a, b, c, d, e, f$. (a,a), (b,b), (c,c), (d,d), (e,e), (f,f), (b,c), (c,b), (b,d), (d,b), (c,d), (d,c), (e,f), (f,e). b) punkty na diagramie: $a,b,c,d,e.$ (a,b), (b,c), (a,c), (d,e). c) punkty na diagramie: $a,b,c,d.$ (b,b), (d,d), (a,b), (a,c), (a,d), (b,c), (b,d), (c,d). d) punkty na diagramie: $a,b,c,d,e,f.$ (a,b), (b,a), (c,d), (d,c), (e,f), (f,e). e) punkty na diagramie: $a,b,c,d,e.$ (a,a), (b,b), (c,c), (d,d), (e,e), (a,b), (b,c), (c,d), (d,e), (e,a). f) punkty na diagramie: $a,b,c,d,e,f.$ (zadnych strzalek) g) punkty na diagramie: $a,b,c,d,e.$ (a,a), (c,c), (a,b), (b,e), (c,b), (b,d). h) punkty na diagramie: $a,b,c,d,e.$ (a,b), (a,c), (c,a), (d,a), (b,d), (d,b), (d,e). i) punkty na diagramie: $a,b,c.$ (a,a), (a,b), (b,c), (c,a). j) punkty na diagramie: $a,b,c,d,e.$ (d,d), (a,b), (a,c), (b,e), (d,c), (c,b). k) punkty na diagramie: $a,b,c,d,e.$ (e,e), (e,a), (a,b), (a,c), (b,c), (c,d), (d,c), (b,d), (d,e). l) punkty na diagramie: $a,b,c,d.$ (a,a), (b,b), (c,c), (d,d), (a,c), (a,b), (b,a), (c,b), (b,c).
tumor postĂłw: 8070	2016-04-26 09:45:40 Relacja jest zwrotna, jeśli dla kaĹźdego punktu x diagramu zawiera (x,x). Na przykład l) jest zwrotna. Nie jest zwrotna j), bo zawiera parę (d,d), ale juĹź nie (a,a) czy (b,b). Relacje f) czy h) sÄ nawet przeciwzwrotne, co znaczy, Ĺźe nie zawierajÄ Ĺźadnej pary (x,x). ---------- Relacja jest symetryczna, jeśli dla kaĹźdej pary (x,y) występuje teĹź (y,x) (oczywiście (x,x) nie trzeba wtedy pisać dwa razy). Relacja l) nie jest symetryczna, bo ma parę (a,c), ale nie ma (c,a). Relacja d) jest symetryczna, bo nie ma Ĺźadnej pary pozbawionej \"lustrzanego odbicia\". Relacja jest słabo antysymetryczna, jeśli Ĺźadna para (x,y) dla róşnych x,y nie ma odpowiednika (y,x). Przy tym relacja słabo antysymetryczna dopuszcza pary (x,x), ktĂłrych by nie dopuszczała asymetryczna. k) nie jest słabo antysymetryczna, bo pojawia się (c,d),(d,c). i) jest słabo antysymetryczna. Gdyby pytanie było jeszcze o asymetrycznÄ , to wtedy by nie była z uwagi na (a,a). ------- Przechodnia jest wtedy, gdy parom (x,y),(y,z) zawsze towarzyszy takĹźe (x,z). Na przykład j) nie jest przechodnia, bo mamy pary (a,b),(b,e), ale nie mamy (a,e). f) jest przechodnia. (Poprzednik implikacji fałszywy, skoro nie ma Ĺźadnych par, więc implikacja zawsze spełniona) Jest przechodnia relacja c) (b,b), (d,d), (a,b), (a,c), (a,d), (b,c), (b,d), (c,d) No bo mamy (a,b),(b,c) oraz (a,c) (a,b),(b,d) oraz (a,d) (a,c),(c,d) oraz (a,d) (b,c),(c,d) oraz (b,d) (Par (b,b) czy (d,d) sprawdzać nie trzeba, bo działajÄ tu analogicznie do elementĂłw neutralnych). Najlepiej wypisz, ktĂłre sÄ zwrotne (dla ćwiczenia teĹź przeciwzwrotne), ktĂłre symetryczne lub słabo antysymetryczne (ale moĹźesz teĹź asymetryczne), no i ktĂłre sÄ przechodnie, a ja sprawdzę przy okazji.
geometria postĂłw: 865	2016-04-27 11:46:48 a) zwrotna, bo kazdy punkt jest w relacji z samym soba symetryczna, bo dla wszystkich punktow spelniona (prawdziwa) jest implikacja xRy $\Rightarrow$ yRx. nie jest slabo antysymetryczna, bo (c,d), (d,c), ale c$\neq$d (implikacja falszywa) przechodnia, bo (b,c), (c,d) oraz (b,d) (c,d), (d,b) oraz (c,b) (d,b), (b,c) oraz (d,c) (c,b), (b,d) oraz (c,d) (d,c), (c,b) oraz (d,b) (b,d), (d,c) oraz (b,c) (e,f), (f,e) oraz (e,e) (f,e), (e,f) oraz (f,f) ------ (e,f) i (f,d), ale f nie jest w relacji z d (poprzednik falszywy, implikacja prawdziwa) b) nie jest zwrotna, bo nie wszystkie punkty (akurat w tym przypadku zadne) sa w relacji z samym soba nie jest symetryczna, bo (a,b), ale b nie jest w relacji z a (implikacja falszywa) slabo antysymetryczna, bo dla par (x,y) nie ma odpowiednika (y,x) (implikacja prawdziwa, bo poprzednik falszywy) przechodnia, bo (a,b), (b,c) oraz (a,c) (d,e) ale e nie jest w relacji z zadnym punktem (implikacja prawdziwa podobnie (b,c) (a,c)) c) nie jest zwrotna, bo nie wszystkie punkty sa w relacji z samym soba (np. punkt a) nie jest symetryczna, bo (a,b) ale nie (b,a) slabo antysymetryczna, bo dla par (x,y) nie ma odpowiednika (y,x) (implikacja prawdziwa, bo poprzednik falszywy) przechodnia d) nie jest zwrotna, bo nie wszystkie punkty sa w relacji z samym soba (np. punkt a) symetryczna nie jest slabo antysymetryczna, bo np. (c,d), (d,c), ale c$\neq$d (implikacja falszywa) nie jest przechodnia, bo (a,b) i (b,a), ale nie (a,a). e) zwrotna, bo kazdy punkt jest w relacji z samym soba nie jest symetryczna, bo (a,b), ale nie (b,a) slabo antysymetryczna, bo dla par (x,y) nie ma odpowiednika (y,x) (implikacja prawdziwa, bo poprzednik falszywy) nie jest przechodnia, bo (a,b) i (b,c), ale nie (a,c) f) nie jest zwrotna, bo zaden punkt nie jest w relacji z samym soba symetryczna slabo antysymetryczna, przechodnia, bo poprzednik falszywy (nie ma zadnej pary), czyli implikacja prawdziwa g) nie jest zwrotna, bo nie wszystkie punkty sa w relacji z samym soba (np. punkt b) nie jest symetryczna, bo (a,b), ale nie (b,a) slabo antysymetryczna, bo dla par (x,y) nie ma odpowiednika (y,x) (implikacja prawdziwa, bo poprzednik falszywy) nie jest przechodnia, bo (a,b) i (b,e), ale nie (a,e) h) nie jest zwrotna, bo nie wszystkie punkty sa w relacji z samym soba (np. punkt b) nie jest symetryczna, bo (a,b), ale nie (b,a) nie jest slabo antysymetryczna, bo np. (a,c), (c,a), ale c$\neq$a (implikacja falszywa) nie jest przechodnia, bo (a,b) i (b,d), ale nie (a,d) i) nie jest zwrotna, bo nie wszystkie punkty sa w relacji z samym soba (np. punkt b) nie jest symetryczna, bo (a,b), ale nie (b,a) slabo antysymetryczna, bo dla par (x,y) nie ma odpowiednika (y,x) (implikacja prawdziwa, bo poprzednik falszywy) nie jest przechodnia, bo (a,b) i (b,c), ale nie (a,c) j) nie jest zwrotna, bo nie wszystkie punkty sa w relacji z samym soba (np. punkt b) nie jest symetryczna, bo (a,b), ale nie (b,a) slabo antysymetryczna, bo dla par (x,y) nie ma odpowiednika (y,x) (implikacja prawdziwa, bo poprzednik falszywy) nie jest przechodnia, bo (d,c) i (c,b), ale nie (d,b) k) nie jest zwrotna, bo nie wszystkie punkty sa w relacji z samym soba (np. punkt b) nie jest symetryczna, bo (a,b), ale nie (b,a) nie jest slabo antysymetryczna, bo (d,c) i (c,d), ale d$\neq$c nie jest przechodnia, bo (d,e) i (e,a), ale nie (d,a) l) zwrotna, bo kazdy punkt jest w relacji z samym soba nie jest symetryczna, bo (a,c), ale nie (c,a) nie jest slabo antysymetryczna, bo (a,b) i (b,a), ale a$\neq$b nie jest przechodnia, bo (c,b) i (b,a), ale nie (c,a) dobrze (szczegolnie uzasadnienia)?
strony: 1 2

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj

© 2019 Mariusz Śliwiński      o serwisie | kontakt   drukuj