Algebra, zadanie nr 5061
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
dominik321 post贸w: 4 |  2016-12-11 20:44:37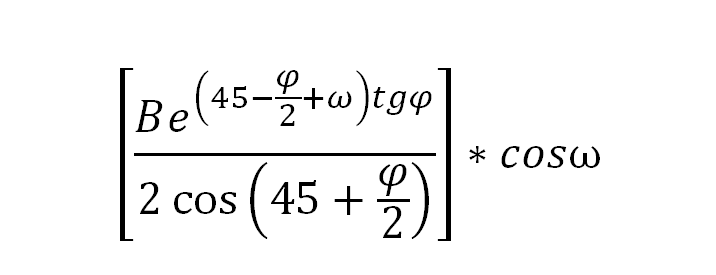 1. Znale藕膰 drug膮 pochodn膮 funkcji, gdzie B,fi to sta艂e, a \omega zmienna. 2. Znale藕膰 ekstreum funkcji. |
janusz78 post贸w: 820 | 2016-12-11 22:12:34 Ze wzor贸w na pochodn膮 funkcji exponent i, pochodn膮 iloczynu dw贸ch funkcji oraz to偶samo艣ci trygonometrycznej na sinus r贸偶nicy dw贸ch argument贸w: $f\'(\omega) = \frac{1}{2\cos(45^{o}+\phi/2)\cos(\phi)}\cdot Be^{(45{0}-\phi/2+\omega)tg(\phi)}\sin(\omega -\phi).$ $ f\'(\omega) = 0,$ gdy $\omega = \phi.$ $f\"(\omega)= \frac{1}{2\cos(45^{o}+\phi/2)\cos^2(\phi)}\cdot Be^{(45^{o}-\phi/2 +\omega)tg(\phi)}\cos(\omega - 2\phi).$ $ f\"(\phi) = \frac{Be^{(45^{o}+\phi/2)tg(\phi)}}{2\cos(45^{o}+\phi/2)\cos^2(\phi)} \cos(-\phi) > 0 $ dla k膮t贸w fazy $-\frac{\pi}{2} <\phi<\frac{\pi}{2}.$ Funkcja $ f $ ma minimum lokalne $ f_{min.lok}= f(\phi).$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj