Geometria, zadanie nr 5789
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
narinaa post贸w: 4 |  2018-08-13 16:25:27Witam, Mam problem z tym zadaniem. Wyznacz najmniejsz膮 warto艣膰 sumy x+2y dla punkt贸w (x,y) nale偶膮cych do wielok膮ta opisanego nier贸wno艣ciami: 4x+y≥22; 15x+5y≥90; 6x+3y≥39; 5x+5y≥35; 6x+12y≥42 Jak zmieni si臋 rozwi膮zanie, gdy dla tego samego wielok膮ta b臋dziemy szuka膰 najmniejszej warto艣ci sumy x+y? |
narinaa post贸w: 4 | 2018-08-13 16:29:04 ehh 4x+y\ge22 15x+5y\ge90 6x+3y\ge39 5x+5y\ge35 6x+12y\ge42 |
chiacynt post贸w: 749 | 2018-08-14 12:11:29 Przepisz zadanie czytelnie w latex\'u |
narinaa post贸w: 4 | 2018-08-15 11:39:37 Wyznacz najmniejsz膮 warto艣膰 sumy x+2y dla punkt贸w (x,y) nale偶膮cych do wielok膮ta opisanego nier贸wno艣ciami: 4x+y$\ge$22; 15x+5y$\ge$90; 6x+3y$\ge$39; 5x+5y$\ge$35; 6x+12y$\ge$42 Jak zmieni si臋 rozwi膮zanie, gdy dla tego samego wielok膮ta b臋dziemy szuka膰 najmniejszej warto艣ci sumy x+y? |
chiacynt post贸w: 749 | 2018-08-15 15:41:19 Jest to zadanie wypuk艂ego programowania liniowego: $ x+2y \rightarrow min $ przy ograniczeniach: $ 4x +y \geq 22,$ $ 3x +y \geq 30,$ $ 2x+y \geq 13.$ $ x +y \geq 7 $ $ x +2y \geq 7.$ Dwa sposoby rozwi膮zania. I spos贸b - graficzny. II spos贸b - Metoda Simpleks. Wiadomo艣膰 by艂a modyfikowana 2018-08-15 18:26:07 przez chiacynt |
narinaa post贸w: 4 | 2018-08-24 21:34:31 Zrobi艂am rysunek ale nie wiem jak dok艂adnie zaznaczy膰 wierzcho艂ki  |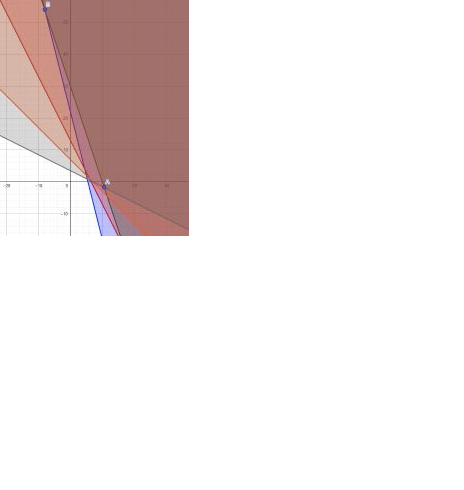
chiacynt post贸w: 749 | 2018-08-25 15:58:11 Trudno mi z tego rysunku odczyta膰 wsp贸艂rz臋dne wierzcho艂k贸w. Wierzcho艂ki wielok膮ta to punkty wsp贸lne przeci臋cia prostych (kraw臋dzi tego wielok膮ta). Nast臋pnie wyznaczamy wektor kierunku funkcji celu: $ \vec{k} = grad(f(x)) = [1, 2].$ Przesuwamy od punktu $ (0,0)$ wzd艂u偶 wielok膮ta prost膮 o wektorze do niej prostopad艂ym $ \vec{k} $. Pierwszy (najbli偶szy) trafiony przez t膮 prost膮 wierzcho艂ek wielok膮ta jest rozwi膮zaniem ZPL. |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj