Inne, zadanie nr 226
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
k_fuzzy post贸w: 5 |  2016-02-02 13:30:28Witam, Mam zagwostk臋 natury geometrycznej. Jak obliczy膰 pole sze艣ciok膮ta nieforemnego. Wszystkie naprzeciwleg艂e boki s膮 r贸wnoleg艂e, jedna para bok贸w o d艂ugo艣ci A a pozosta艂e cztery boki o d艂ugo艣ci B. Nie wiemy ile wynosz膮 d艂ugo艣ci bok贸w, nie znamy miar 偶adnych k膮t贸w a jedyne co znamy to odleg艂o艣ci naprzeciwleg艂ych bok贸w od siebie (nazwijmy je A i B (dwie odleg艂o艣ci b臋d膮 takie same)). Czekam na propozycje odpowiedzi. |
tumor post贸w: 8070 | 2016-02-02 13:36:42 Edit: Przepraszam, za pierwszym razem niedok艂adnie czyta艂em tre艣膰. Czy A i B to d艂ugo艣ci bok贸w, czy odleg艂o艣ci mi臋dzy bokami le偶膮cymi naprzeciw siebie? Wiadomo艣膰 by艂a modyfikowana 2016-02-02 16:39:20 przez tumor |
k_fuzzy post贸w: 5 | 2016-02-02 14:42:46 hmmm... ale my nie znamy ani d艂ugo艣ci boku, ani k膮ta... |
k_fuzzy post贸w: 5 | 2016-02-02 19:45:36 Moja wina! Nazwa艂em zar贸wno boki jak i odleg艂o艣ci mi臋dzy bokami tymi samymi literami. No wi臋c niech d艂ugo艣ci bok贸w nazywaj膮 si臋 A i B - i nie s膮 nam one znane. Odleg艂o艣ci pomi臋dzy naprzeciwleg艂ymi bokami zawijmy X i Y. I te warto艣ci znamy. Czy jeste艣my w stanie obliczy膰 pole takiego sze艣ciok膮ta? |
k_fuzzy post贸w: 5 | 2016-02-03 11:13:56 Dla rozja艣nienie przesy艂am rysunek. X i Y - znane, A i B - nie znane  |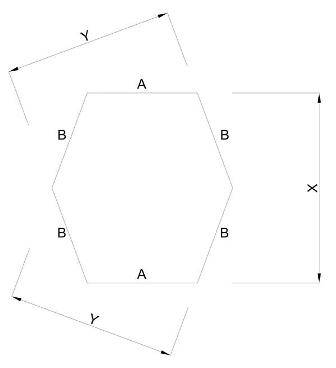
tumor post贸w: 8070 | 2016-02-03 12:21:52 Okejka, tu mo偶emy co艣 powiedzie膰. Narysuj sobie okr膮g o 艣rednicy Y, a tak偶e dwie r贸wnoleg艂e proste k,l (sugeruj臋 - poziome) odleg艂e od 艣rodka okr臋gu o $\frac{X}{2}$, czyli wzajemnie od siebie o X. Niech $X>Y*\sqrt{2}$, tak dla wi臋kszej oczywisto艣ci. Teraz zr贸b dwie figury. Jedna to b臋dzie romb opisany na okr臋gu, kt贸rego dwa wierzcho艂ki umie艣膰 na prostych k,l. Druga figura to prostok膮t, kt贸rego dwa boki le偶膮 na prostych k,l, a dwa s膮 styczne do okr臋gu. Pola tych figur to dla rombu: $Xasin\alpha$, gdzie $a$ jest bokiem rombu, natomiast $\alpha$ jest k膮tem mi臋dzy przek膮tn膮 X i bokiem a, dla prostok膮ta XY. R贸wne b臋d膮 tylko, gdy $Y=a\sin\alpha$. Zauwa偶my jednak, 偶e kr贸tsza przek膮tna rombu, oznaczmy j膮 $Z$, jest kr贸tsza ni偶 $Y\sqrt{2}$, wobec tego $sin\alpha=\frac{\frac{1}{2}Z}{a}<\frac{\frac{1}{2}Y\sqrt{2}}{a}<\frac{Y}{a}$, wobec tego pole rombu jest w tej sytuacji mniejsze ni偶 pole prostok膮ta. A teraz wr贸膰my do naszych sze艣ciok膮t贸w. Mo偶emy znale藕膰 sze艣ciok膮t o dowolnym polu mi臋dzy polami rombu i prostok膮ta, poniewa偶 przekszta艂caliby艣my te figury w spos贸b ci膮g艂y. Skoro zatem przy zadanym X i Y mog膮 istnie膰 sze艣ciok膮ty o r贸偶nych polach, to zadanie rozwi膮zania jednoznacznego mie膰 nie b臋dzie. Wprowadzi艂em tu dodatkowe warunki, np $X>Y\sqrt{2}$, 偶eby skorzysta膰 z prostszych przekszta艂ce艅. Przy pewnych danych pole prostok膮ta i rombu b臋d膮 identyczne, co zmieni nieco konstrukcj臋 wywodu. W og贸lno艣ci jednak zadanie to rozwi膮zania nie ma i potrzeba dodatkowych danych. ---- Inaczej to samo rozumowanie: Narysuj 膰wier膰 okr臋gu o promieniu Y/2 oraz tr贸jk膮t prostok膮tny, kt贸rego przyprostok膮tne pokrywaj膮 si臋 z ramionami naszego wycinka ko艂a, a przeciwprostok膮tna jest styczna do 艂uku. Niech $\alpha$ b臋dzie k膮tem mi臋dzy promieniem opadaj膮cym na punkt styczno艣ci a wybran膮 przyprostok膮tn膮. Na jednej z przyprostok膮tnych od艂贸偶 odcinek X/2. Znaj膮c $\alpha$ mo偶emy wyznaczy膰 dowolne odcinki w tr贸jk膮cie, mo偶emy zatem wyznaczy膰 te偶 pole trapezu, kt贸ry zostanie przed odci臋cie tego, co wystaje poza nasze X/2. Ten trapez jest 膰wiartk膮 opisanego w zadaniu sze艣ciok膮ta. Mo偶na pokaza膰, 偶e pole trapezu zale偶y od wyboru k膮ta $\alpha$, czyli dane z zadania s膮 niewystarczaj膮ce dla podania pola sze艣ciok膮ta. Wiadomo艣膰 by艂a modyfikowana 2016-02-03 12:24:08 przez tumor |
k_fuzzy post贸w: 5 | 2016-02-03 13:56:06 Dzi臋ki bardzo za pomoc! |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj