Inne, zadanie nr 27
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
mpaolo post贸w: 12 |  2011-12-03 00:38:48oblicz obj臋to艣膰 bry艂y powsta艂ej w wyniku obrotu sze艣cianu wok贸艂 jego przek膮tnej |
agus post贸w: 2387 | 2011-12-03 23:49:43 Przek膮tna sze艣cianu jest przek膮tn膮 trzech przekroj贸w w kszta艂cie prostok膮ta o bokach a i a$\sqrt{2}$. Odleg艂o艣膰 wierzcho艂k贸w sze艣cianu, kt贸re nie s膮 ko艅cami przek膮tnej sze艣cianu od tej przek膮tnej jest taka sama i wynosi 1/3*a$\sqrt{6}$ (jest to wysoko艣膰 tr贸jk膮ta prostok膮tnego o przyprostok膮tnych a i a$\sqrt{2}$oraz przeciwprostok膮tnej a$\sqrt{3}$, wychodz膮ca z wierzcho艂ka k膮ta prostego, wyliczona z zale偶no艣ci: 1/2*a*a$\sqrt{2}$=1/2*a$\sqrt{3}$*h ) Jest 6 takich odcink贸w, po 2 le偶膮 w jednej p艂aszczy藕nie, a po trzy le偶膮 w r贸偶nych p艂aszczyznach, ale dochodz膮 do tego samego punktu na przek膮tnej sze艣cianu. Rysunek-prostok膮t o bokach a i a$\sqrt{2}$z przek膮tn膮,zaznaczone odleg艂o艣ci wierzcho艂k贸w, kt贸re nie s膮 ko艅cami przek膮tnej od przek膮tnej,odleg艂o艣ci dziel膮 przek膮tna na trzy r贸wne cz臋艣ci x, co wynika z obliczenia: $x^{2}$=$a^{2}$-(1/3*a$\sqrt{6}$)^2 x=1/3*a$\sqrt{3}$ Z obrotu sze艣cianu wok贸艂 przek膮tnej powstanie bry艂a z艂o偶ona z walca i z艂膮czonych z nim podstaw膮 sto偶k贸w. Walec i sto偶ki maj膮 ten sam promie艅 i t臋 sam膮 wysoko艣膰: r=1/3*a$\sqrt{6}$ h=1/3*a$\sqrt{3}$ zatem obj臋to艣膰 bry艂y wynosi (1+2*1/3)*$\pi$*(1/3*$\sqrt{6}$)^2 *1/3*a$\sqrt{3}$ czyli 10/27*$\sqrt{3}$*$\pi$*$a^{3}$ |
mpaolo post贸w: 12 | 2011-12-12 20:21:53 Bardzo dzi臋kuj臋 za jedyn膮 odpowied藕, jednak wydaje mi si臋, 偶e wspomniany walec faktycznie jest czym艣 co przypomina felg臋 samochodow膮. Wida膰 to dok艂adniej obracaj膮c do艣wiadczalnie model sze艣cianu. Czy te zakrzywienia s膮 fragmentami paraboli? Je艣li kto艣 wie, to prosz臋 potwierdzi膰, bez dowodu, bo szkoda pisania. Interesowa艂by mnie ostateczny wynik :) |
struktor post贸w: 9 | 2011-12-22 23:26:27 Dok艂adniej jest to bry艂a z艂o偶ona z dw贸ch sto偶k贸w i kawa艂ka hiperboloidy obrotowej mi臋dzy nimi. Informacje potrzebne do rozwi膮zania zadania znajdziesz na tej stronie: http://mathworld.wolfram.com/Cube.html ==================================================== Szukana bry艂a jest przedostatni膮 w szeregu:  |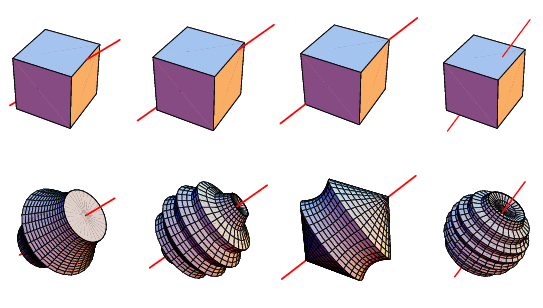
mpaolo post贸w: 12 | 2011-12-23 21:51:35 Wielkie dzi臋ki za fachow膮 literatur臋 :) nie ma to, jak wymy艣li膰 sobie zadanie i troch臋 si臋 z nim pom臋czy膰 ;p |
struktor post贸w: 9 | 2011-12-24 09:51:02 Ciesz臋 si臋, 偶e mog艂em troch臋 skr贸ci膰 te m臋czarnie ;P Na cytowanej stronie, s膮 te偶 wyniki oblicze艅 po艂o偶enia osi obrotu przechodz膮cej przez 艣rodek sze艣cianu, daj膮cej najwi臋ksz膮 obj臋to艣膰 powsta艂ej bry艂y obrotowej. |
mpaolo post贸w: 12 | 2011-12-24 15:35:28 W艂a艣nie to mia艂o by膰 moje nast臋pne pytanie :) Bodaj偶e jest to ta ostatnia bry艂a powy偶ej, ale musz臋 jeszcze doczyta膰. |
mpaolo post贸w: 12 | 2011-12-24 16:37:59 wracaj膮c do poprzednich oblicze艅 obj臋to艣膰 bry艂y (z obrotu sze艣cianu o boku a) wynosi 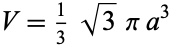 z czego stosunek obj臋to艣ci sto偶ek:hiperboloida:sto偶ek wynosi 2:5:2? w \"najw臋偶szym miejscu\" hiperboloida ma promie艅 1/2$\sqrt{2}$a czy 1/3$\sqrt{3}$a? |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj