Inne, zadanie nr 97
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
tomnow post贸w: 10 |  2012-09-22 20:54:38Witam Mam do pokolorowania $n$-k膮t foremny za pomoc膮 $k$ kolor贸w. N-k膮t jest podzielony na n cz臋艣ci odcinkami wychodz膮cymi ze 艣rodka okr臋gu opisanego na danym n-k膮cie do jego wierzcho艂k贸w. Pytanie: Ile jest r贸偶nych kolorowa艅 takiego wielok膮ta? Nale偶y przyj膮膰, 偶e je艣li w wyniku obrotu lub \"odwr贸cenia\" figury na drug膮 stron臋 otrzymamy figur臋 podobn膮 to uznajemy kolorowania za takie same. Rysunek ni偶ej przedstawia kolorowanie czworok膮ta przy u偶yciu dw贸ch r贸偶nych kolor贸w. Jest ich 6. 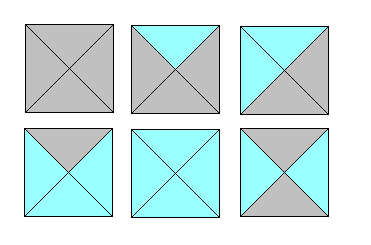 No i tu moja wyobra藕nia si臋 ko艅czy  . Czy jest jaki艣 wz贸r og贸lny, kt贸ry m贸g艂by okre艣li膰 liczb臋 kolorowa艅 n-k膮t贸w za pomoc膮 k kolor贸w? |
tumor post贸w: 8070 | 2012-10-23 20:36:02 Odpowiedzi膮 na Twoje pytanie jest Lemat Burnside\'a. $N=\frac{1}{|G|}\sum_{g\in G}|fix(g)|$ $N$ to jest liczba, kt贸rej szukasz. $G$ jest grup膮 operacji, kt贸rymi dzia艂asz na zbiorze. Konkretnie chodzi nam o grup臋 izometrii wielok膮ta foremnego. W grupie tej dla kwadratu mamy obroty o $0,90,180,270$ stopni oraz symetrie wzgl臋dem przek膮tnych (dwie) i wzgl臋dem symetralnych bok贸w (te偶 dwie). Zatem $|G|=8$. Dla pewno艣ci dopisz臋, 偶e $G$ jest grup膮 w sensie teorii grup, algebry, nie tak膮 sobie zbieranin膮. :) $fix(g)$ to zbi贸r punkt贸w sta艂ych przekszta艂cenia $g$, czyli w naszym przypadku to zbi贸r kolorowa艅, kt贸rych przekszta艂cenie $g$ nie zmieni. 1) Obr贸t o $0^\circ$ Taki obr贸t zostawia kwadrat w spokoju. Wszystkich mo偶liwo艣ci pokolorowania kwadratu k kolorami jest k^4, a gdy pokolorujemy, to obr贸t nic nie zmieni. Dlatego WSZYSTKIE mo偶liwe kolorowania s膮 punktami sta艂ymi. 2) Obr贸t o $90^\circ$ lub $270^\circ$ Zauwa偶my, 偶e kwadrat musi by膰 ca艂y w jednym kolorze, by po takim obrocie pozosta艂 niezmieniony. Zatem punkt贸w sta艂ych jest tyle, ile kolor贸w, czyli $k$. 3) obr贸t o $180^\circ$ By nie zmieni艂 on kwadratu, identyczne musz膮 by膰 tr贸jk膮ty naprzeciw siebie. Kwadrat mo偶e by膰 dwukolorowy, by by艂 punktem sta艂ym takiego przekszta艂cenia, ale nie dowolnie dwukolorowy, tylko z identycznymi odpowiednimi tr贸jk膮tami, czyli $k^2$ mo偶liwo艣ci. 4) symetria wzgl臋dem przek膮tnej Tu tak偶e $k^2$ mo偶liwo艣ci. 5) symetria wzgl臋dem symetralnej boku kwadratu Te tr贸jk膮ty, kt贸re s膮 po przeciwnych stronach osi symetrii, musz膮 by膰 w tych samych kolorach. Natomiast te przeci臋te osi膮 symetrii mog膮 by膰 dowolne, czyli $k^3$. Og贸艂em, dla $k$ kolor贸w i kwadratu, dostajemy $N=\frac{1}{8}(k^4+2k^3+3k^2+2k)$ Co jest rzeczywi艣cie (uff!) r贸wne $6$, je艣li mamy dwa kolory. ---- W og贸lnym przypadku bierzesz n-k膮t. Dzielisz go na n tr贸jk膮t贸w, wszystkich mo偶liwych kolorowa艅 $k$ kolorami masz $k^n$. Rozwa偶asz sobie wszystkie przekszta艂cenia, kt贸re musz膮 tworzy膰 grup臋. Same obroty tworz膮 grup臋, ale obroty z symetriami te偶 tworz膮 grup臋 i w tym przypadku na niej si臋 skupimy. Dla n-k膮ta foremnego masz $n$ obrot贸w o kolejne wielokrotno艣ci $\frac{360^\circ}{n}$. Symetrii jest $n$ (dla nieparzystego $n$ osiami s膮 symetralne bok贸w, dla parzystego symetralne bok贸w i przek膮tne 艂膮cz膮ce przeciwleg艂e wierzcho艂ki). Dla obrotu o $0$ stopni oczywi艣cie wszystkie kolorowania s膮 punktami sta艂ymi. Dla obrotu o $\frac{360^\circ}{n}$ punktami sta艂ymi s膮 tylko wielok膮ty jednokolorowe. Og贸lniej, je艣li $NWD(p,n)=1$, to obr贸t o $p\frac{360^\circ}{n}$ ma punkty sta艂e tylko w postaci n-k膮t贸w jednokolorowych, czyli jest ich $k$. I tak dalej, i tak dalej, mo偶na te rozwa偶ania prowadzi膰, ale mi si臋 pisa膰 nie chce. Pomy艣l, kt贸re tr贸jk膮ty z kt贸rymi musz膮 mie膰 identyczny kolor, by w obrotach czy symetriach kolorowa艅 nie zmieni膰. W ten spos贸b ustal ilo艣膰 kolorowa艅, kt贸re w tych przekszta艂ceniach s膮 punktami sta艂ymi. A potem to ju偶 do wzoru. :) |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj