logowanie

Funkcja potęgowa

Funkcją potęgową o wykładniku n nazywamy funkcję określoną wzorem f(x) = xⁿ.

Dziedzina funkcji potęgowej zależy od wykładnika n.

Jeżeli n jest liczbą naturalną, wtedy f jest funkcją wielomianową, a jej dziedziną jest zbiór liczb rzeczywistych.

Wykres funkcji f(x) = xⁿ

Dla n = 2k, gdzie k ∈ N⁺

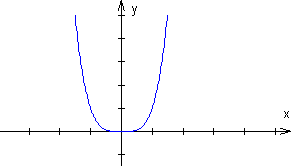
Dla n = 2k - 1, gdzie k ∈ N⁺

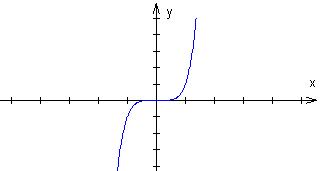
Dla n = 2k, gdzie k ∈ Z^-

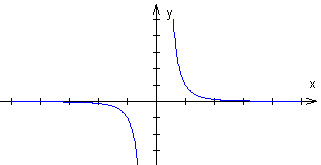
Dla n = 2k - 1, gdzie k ∈ Z^- ∪ {0}

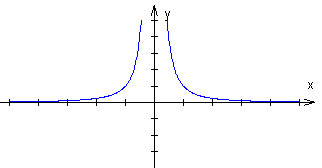
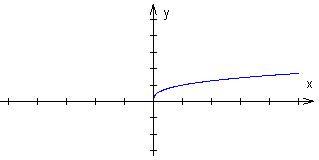
Dla $n=\frac{1}{k}$, gdzie k ∈ {2, 3, 4, ...}

Jeżeli n jest liczbą całkowitą parzystą, to funkcja potęgowa f(x) = xⁿ jest parzysta.
Jeżeli n jest liczbą całkowitą nieparzystą, to funkcja potęgowa f(x) = xⁿ jest nieparzysta.

© 2024 math.edu.pl      kontakt