Kąty naprzemianległe i odpowiadające

Jeżeli dwie proste położone na płaszczyźnie, przetniemy trzecią, którą nazywamy wówczas prostą sieczną, to utworzy się osiem kątów, mających następujące nazwy:

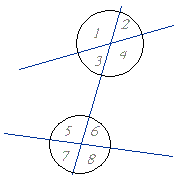
Kąty 3 i 6 oraz 4 i 5 - kąty naprzemianległe wewnętrzne
Kąty 1 i 8 oraz 2 i 7 - kąty naprzemianległe zewnętrzne
Kąty 1 i 5, 3 i 7, 2 i 6, 4 i 8 - kąty odpowiadające
Kąty 3 i 5, 4 i 6 - kąty jednostronne wewnętrzne
Kąty 3 i 5, 4 i 6 - kąty jednostronne wewnętrzne

Twierdzenie

Jeśli dwie proste z dowolną sieczną tworzą:
- kąty naprzemianległe zewnętrzne równe,
- kąty odpowiadające równe,
to te proste są równoległe.

Twierdzenie odwrotne

Jeżeli dwie proste równoległe, przetniemy dowolną prostą sieczną, to kąty naprzemianległe i odpowiadające są sobie równe.

Postulat Euklidesa

Twierdzenie w tym brzmieniu przyjął Euklides za pewnik w swojej teorii prostych równoległych. Ten właśnie pewnik, czyli tzw. XI pewnik Euklidesa znany jest w geometrii pod nazwą postulatu Euklidesa o prostych równoległych.