Różnica symetryczna zbiorów
Różnicę symetryczną zbiorów A i B nazywamy zbiór składający się z elementów należących do dokładnie jednego ze zbiorów A i B.
Inaczej różnica symetryczna zbiorów A i B, to zbiór elementów, które należą do zbioru A lub do zbioru B, ale nie należą do obydwu naraz. Różnicę symetrycznych zbiorów A i B oznaczamy A÷B. Z definicji różnicy symetrycznej zbiorów wynika, że x jest elementem zbioru A÷B wtedy i tylko wtedy, gdy jest elementem zbioru A i nie jest elementem zbioru B lub gdy jest elementem zbioru B i nie jest elementem zbioru A.
Warunek konieczny i dostateczny na to, aby x ∈ A÷B zapisujemy w sposób
następujący:
(x∈A÷B) ⇔
((x∈A ∧ x∉B)
∨ (x∉A ∧ x∈B)).
Różnicę symetryczną zbiorów A\B można przedstawić graficznie jako obszar zacieniowany:
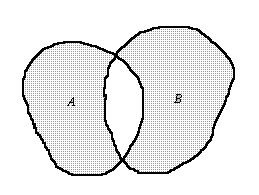
Dla różnicy symetrycznej zbiorów zachodzi A÷B = (A\B) ∪ (B\A)