Argument liczby zespolonej

Znając moduł liczby zespolonej, możemy liczbę zespoloną opisać nie tylko za pomocą punktu - ale także za pomocą, wektora o początku w punkcie (0,0) i końcu w punkcie o współrzędnych liczby zespolonej. Jednak dla pewnych punktów odległość od początku układu współrzędnych płaszczyzny zespolonej będzie taka sama, ponieważ w przypadku płaszczyzny zespolonej wodząc wektorem o znanej długości zakreślimy okrąg o promieniu r = |z|. Z pomocą przychodzą własności trójkąta prostokątnego oraz twierdzenie sinusów i twierdzenie cosinusów. Dzięki nim można wyznaczyć kąt φ pomiędzy wektorem oraz osią rzeczywistą. Argument liczby zespolonej jest więc to miara kąta skierowanego między wektorem reprezentującym liczbę zespoloną z = a + bi na płaszczyźnie zespolonej a osią rzeczywistą.

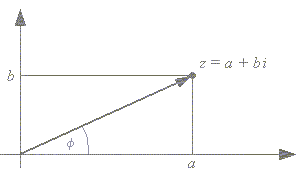
argument liczby zespolonej

Argumentem liczby zespolonej z = a + bi ≠ 0 nazywamy każdą liczbę rzeczywistą φ spełniającą dwa warunki:
$\cos φ = \frac{a}{| z |} i \sin φ = \frac{b}{| z |}$ .

Argument φ liczby zespolonej z oznacza się φ = arg z.

Pierwszym ramieniem kąta skierowanego jest dodatnia półoś rzeczywista, drugie ramię jest wyznaczone przez wektor Oz. Każda liczba zespolona ma nieskończenie wiele argumentów, co jest konsekwencją okresowości funkcji sinus i cosinus. Inaczej wodząc wektorem po okręgu, możemy wykonać wiele obrotów, dlatego wprowadzono argument główny liczby zespolonej, który mieści się w przedziale od 0° do 360°

Argumentem głównym liczby zespolonej z ≠ 0 nazywamy tę spośród liczb arg z, która spełnia nierówność 0 ≤ arg z < 2π.

Układ współrzędnych, w którym podajemy współrzędne modułu liczby zespolonej i jej argumentu: (|z|, φ) nazywamy układem współrzędnych biegunowych, a współrzędne - współrzędnymi biegunowymi. Wykorzystując do określenia położenia punktu (a, b) układ współrzędnych biegunowych otrzymamy tzw. postać trygonometryczną liczby zespolonej z = |z|(cosφ + isinφ), gdzie φ = arg z.