Liczby zespolone

Czym są liczby zespolone? Liczby zespolone pojawiły się jako rozwiązania równań kwadratowych. Można zastanawiać się jakie są rozwiązania równania x² + 1 = 0? Jeśli ma ono rozwiązanie, musi być nim liczba, której kwadrat wynosi -1. Ale kwadrat każdej liczby rzeczywistej jest dodatni. Jeśli chcemy, by mimo wszystko powyższe równanie miało jakieś rozwiązanie, trzeba wymyślić jakieś nowe liczby, których kwadrat byłby ujemny.

Tak uczyniono i do liczb rzeczywistych dodano liczby urojone, stworzone specjalnie po to, by uzyskać kwadrat ujemny! Nowy byt matematyczny nazwano imaginarius, oznaczono pierwiastek z liczby -1 literą i oraz określono działania, aby móc liczyć. I tak powstały liczby zespolone. Oznaczamy symbolicznie C.

Liczby zespolone zatem to pary uporządkowanych (a, b) liczb rzeczywistych a i b, dla których określone są działania dodawania i mnożenia:
(a, b) + (c, d) = (a + c, b + d)
(a, b)(c, d) = (ac - bd, ad + bc)

W zapisie z = (a, b) a nazywamy częścią rzeczywistą, natomiast b częścią urojoną liczby zespolonej z. Zapisujemy re z = a oraz im z = b.

Liczby rzeczywiste stają się szczególnymi liczbami zespolonymi, takimi, których część urojona b jest zerem. Jeśli chodzi o liczby zespolone, których część rzeczywista a wynosi zero, są to liczby urojone. Kwadrat czystej liczby urojonej jest ujemny!
Liczby zespolone postaci (0, b) nazywamy jednostką urojoną i oznaczamy (0, b) = i. Liczba ta ma szczególną własność, a mianowicie i · i = (0, 1)(0, 1) = (-1, 0) = -1, co oznacza, że i² = -1. Stworzony w ten sposób formalizm pozwala odnaleźć pierwotną ideę dotyczącą tego urojonego bytu, którego kwadrat jest ujemny.
Ponieważ (b, 0)(0, 1) = (0, b), to każdą liczbę zespoloną z = (a, b) można zapisać w postaci z = (a, b) = (a, 0) + (b, 0)(0, 1) = a + bi, która jest postacią algebraiczną liczby zespolonej.

Liczbę zespoloną postaci (a, -b) nazywamy liczbą sprzężoną z liczbą zespoloną z = (a, b) i oznaczamy z.

Droga liczb zespolonych była długa, trzeba było kilku wieków, by te nowe liczby uzyskały prawo do matematycznego istnienia. W 1545 roku Girolamo Cardano jako pierwszy złamał zakaz, zapisując pierwiastek ujemny. W 1777 roku Leonhard Euler w miejsce $\sqrt{- 1}$ , wprowadził symbol i, który oznacza jednostkę urojoną wynoszącą pierwiastek z minus jeden.

Płaszczyzna zespolona

Liczba rzeczywista opisuje w istocie odległość opatrzoną kierunkiem wskazanym przez jej znak, mierzoną za pomocą pewnej ustalonej jednostki. Dla liczb rzeczywistych istnieją tylko dwa kierunki: w lewo lub w prawo wzdłuż ustalonej prostej. Podobnie możemy określić liczby zespolone jako odległości w dowolnym kierunku, ale na ustalonej płaszczyźnie. Liczba zespolona jest punktem na płaszczyźnie wraz z wyróżnionym odcinkiem skierowanym o długości jednej jednostki.

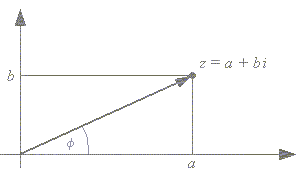
Każdej liczbie zespolonej z = a + bi odpowiada na płaszczyźnie punkt o współrzędnych (a, b) lub wektor o współrzędnych , zaczepiony w początku układu współrzędnych. Liczba i jest położona na osi urojonej w odległości 1 od punku przecięcia. Wyraża ją para (0,1).

Liczba zespolona z = a + bi przedstawiona przez wektor, łączy pojęcie wielkości z pojęciem kierunku, co otwiera przed liczbami tymi ogromne pole zastosowań. Natomiast czymś, co zostało utracone jest możliwość porównywania liczb. Dwie liczby rzeczywiste są zawsze porównywalne, nie jest to już prawdziwe w przypadku liczb zespolonych. Dwie liczby zespolone są nieporównywalne.

Działania na liczbach zespolonych

Dodawanie
(a₁ + b₁i) + (a₂ + b₂i) = (a₁ + a₂) + (b₁ + b₂)i

Odejmowanie
(a₁ + b₁i) - (a₂ + b₂i) = (a₁ - a₂) + (b₁ - b₂)i

Mnożenie
(a₁ + b₁i)(a₂ + b₂i) = (a₁a₂ - b₁b₂) + (a₁b₂ + a₂b₁)i

Dzielenie
$\frac{(a_{1} + b_{1} i)}{(a_{2} + b_{2} i)} = \frac{a_{1} a_{2} + b_{1} b_{2}}{a_{2}^{2} + b_{2}^{2}} + \frac{b_{1} a_{2} - a_{1} b_{2}}{a_{2}^{2} + b_{2}^{2}}$
Przy dzieleniu liczb zespolonych należy uwolnić mianownik od liczby zespolonej, mnożąc licznik i mianownik przez liczbę sprzężoną z dzielnikiem.

Moduł liczby zespolonej (wartość bezwzględna)
Argument liczby zespolonej

Wzór de Moivre'a

Wzór de Moivre'a jest wzorem na n-tą potęgę liczby zespolonej zapisanej w postaci trygonometrycznej.
Jeżeli z = |z|(cosφ + isinφ) oraz n należy do zbioru liczb całkowitych, to:
zⁿ = |z|ⁿ(cos(nφ) + isin(nφ)).