Pentagon liczb pierwszych. Prime number pentagon.
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Wiadomo艣膰 |
sylvi91 post贸w: 23 |  2017-10-10 10:22:37 2017-10-10 10:22:37Witam. To m贸j pierwszy post na forum. Zarejestrowa艂em si臋 aby przedstawi膰 szanownym forumowiczom pewne zagadnienie zwiazane z liczbami pierwszymi i nie tylko. Rozk艂ad w przestrzeni 2D za pomoc膮 Spirali Ulama oraz Krzy偶a Plichty zainspirowa艂 mnie do troch臋 innej wariacji z liczbami pierwszymi w przestrzeni. Liczby pierwsze w geometrii na p艂aszczy藕nie. Chcia艂bym zaprezentowa膰, 偶e tak powiem - metod臋 rozstawienia liczb pierwszych. Nazwa艂em j膮 \"rozstawieniem pentagonalnym\". Pomys艂 jest bardzo prosty. Nale偶y rozstawi膰 na wierzcho艂kach pi臋ciok膮t贸w kolejne liczby naturalne. (czyli 1,2,3,4,5,6,7 itd.) Liczby pierwsze b臋d膮 rozchodzi艂y si臋 z do艣膰 ciekaw膮 regularno艣ci膮. Ka偶da liczba pierwsza na danym kierunku (z danego k膮ta tego pi臋ciok膮ta). b臋dzie wi臋ksza od poprzedniej o dziesietn膮 warto艣膰 wynosz膮c膮 5, 10, 20, 30 i tak dalej. Ka偶da kolejna liczba pierwsza zachowa warto艣膰 jedno艣ci tak膮 sam膮 jak poprzednia liczba. Na przyk艂ad: 2, 7, 17, 37, 47, 67, 97, 107 i tak dalej. (wyj膮tkiem jest pierwsza liczba pierwsza czyli 2). To jest oczywista regularno艣膰. To jest pewien wz贸r w zbiorze liczb pierwszych. Moim zdaniem ta regularno艣c wynika z w艂a艣ciwo艣ci pi臋ciok膮ta, w kt贸rym k膮t jego ramion to 108 stopni. W pi臋ciok膮cie, jego obw贸d do przek膮tnej (ale nie tej przechodz膮cej przez geometryczny 艣rodek) ma stosunek wynosz膮cy Phi. (1.618). Phi jest z艂ot膮 liczb膮 stosowan膮 w z艂otym podziale. To wskazuje moim zdaniem na zwi膮zek zbioru liczb pierwszych ze z艂otym podzia艂em. Wskazuje te偶, 偶e nie ma przypadkowo艣ci w tym zbiorze liczb pierwszych. Eksperyment dokona艂em na pierwszych 500 liczbach naturalnych i s膮dz臋, 偶e ta prawid艂owo艣c wyst臋puje do niesko艅czono艣ci. Mo偶e kogo艣 to zainspiruje do dalszych prac na tymi liczbami i/lub oka偶e si臋 wog贸le pomocne. Nigdzie dotychczas nie znalaz艂em nawet podobnego rysunku dotycz膮cego liczb pierwszych, opisanych na pentagonie. (pi臋ciok膮cie). Pan Stanis艂aw Ulam stworzy艂 kwadratow膮 spiral臋, kt贸r膮 zachwyci艂 si臋 ca艂y 艣wiat. A co my艣licie o mojej pentagonalnej spirali? W podanym poni偶ej linku jest program dla windows - jego bardzo \"surowa\" wersja. Obs艂uga te偶 jest toporna. Przesuwaj膮c myszk膮 mamy wp艂yw na przesuwanie obrazu, a klawiszami strza艂ek manipulujemy rysowanym przez algorytm programu geometrycznym wzorem. Uwaga. Aplikacji nie skanowa艂em na obecno艣膰 wirus贸w. Program rysuje spiral臋 z zachowaniem kszta艂u pi臋ciok膮ta w przestrzeni 2D i zaznacza na wierzcho艂kach liczby naturalne kolorem bia艂ym, oraz wyst臋puj膮ce liczby pierwsze kolorem czarnym. R贸wnie dobrze m贸g艂y rysowa膰 same pi臋ciok膮ty rozmieszczone centrycznie i na ka偶dym kolejnym ustawia膰 liczby naturalne i zaznacza膰 liczby pierwsze. To jest 0.3 beta w wersji specjalnej dla Matematyka.pl 艢wiat toczy si臋 na kole, kt贸rym rz膮dzi pentagon. ...USA Pentagon? ;) Wersja angielska. ... Pentagon of prime numbers. Or. Prime numbers pentagon. PNP Prime numbers in simple 2D geometry. I would like to presents method of distribution prime numbers. I called this method “pentagonal distribution”. The idea is very simple. Let’s distribute natural numbers on vertexes of pentagonal shape. The prime numbers will be aligned in four directions with some kind of regularity. Except number 5. Each prime number on exact direction will be bigger than previous prime number by decimal value 5, 10, 20, 30 or so. And each number will keep the units value exact same as previous number. For example: numbers 2, 7, 17, 37, 47, 67, 97... and more are prime numbers on one vertex. (exception is first number) It’s obvious regularity. It’s a pattern i a prime numbers. I think it is possible, because in pentagon circumference to diagonal is ratio equal to number Phi. Phi i a number from golden ratio. So. This is another way to find interesting behavior of prime numbers in 2D space. Another than square Ulam Spiral or Plichta Cross. This program is actually drawing pentagonal shaped spiral. ... World is turning on wheel and Pentagon rulez! ;) USA Pentagon? ... Below link to program. \" Pentagon of prime numbers\" and screenshot. Author: Sylwester Bogusiak aka Sylvi91. This program is in 0.3 beta version Special Edition for Matematyka.pl This program is shared without any warrany. This program is using Allegro library by Shawn Hargreaves. Link do programu. https://drive.google.com/open?id=0BzPu8lykW13mQ2ItTkNteEg2a0U Widok na dzia艂aj膮cy program... a w艂a艣ciwie fragment narysowanej spirali. https://drive.google.com/file/d/0BzPu8lykW13mNHJUdWh2MkZVYnM/view?usp=sharing Pozdrawiam. |
nk_1 post贸w: 14 |  2017-11-19 09:20:13 2017-11-19 09:20:13W cely zwi臋kszenia zakresu liczb pierwszych mo偶e przyda si臋 inny spos贸b generowania liczb pierwszych pokazany poni偶ej. Pozwala na o wiele wi臋kszy zakres analizy liczb pierwszych np. w Excelu. Sito Ma艂gorzaty opisane pod linkiem: https://1drv.ms/b/s!AsqwpKK-51whhhzzvgOxdib8Y_rW Makro w Excelu pozwala na przygotowanie zbiory liczb pierwszych do analizy: Sub sito() Dim j, i As Long Dim a, b As Long Dim t As Boolean Dim f As Boolean Dim x_max As Long Dim x As Long Dim yp As Long Dim pk As Integer Dim pky As Integer Dim pk_max As Integer Dim pk_min As Integer Range(\"B:Z\").ClearContents \'ilo栤danych w kadej kolumnie np. 1040000 x_max = Range(\"A1\").Text \'ilo栫olumn - warto栭ax 25 pk_max = Range(\"A2\").Text \' zaczynamy od 2 kolumny pk = 2 pky = 2 pk_min = 2 pk_max = pk_max + 1 t = True \' warto栰ocztkowa dla iteracji yp = 1 i = 0 Do i = i + 1 \' warto栰ocztkowa x dla danej iteracji i x = yp \' wyliczenie wartosci a i b a = 1 + 2 * i If t Then b = 4 * i + 3 Else b = 4 * i + 1 End If \' ustawienie kolejnoci a czy b - t dla iteracji i , f dla poditeracji f = t If Cells(i, pk).Value <> 1 Then If f Then x = x + b yp = x + a Else x = x + a yp = x + b End If \'zaznaczenie elementla danej iteracji For j = pk_min To pk_max Do While x < x_max Cells(x, j) = 1 If f Then x = x + a Else x = x + b End If f = Not (f) Loop x = x - x_max + 1 Next j Else yp = yp + a + b End If If Not (yp < x_max) Then yp = yp - x_max + 1 pky = pky + 1 End If pk_min = pky t = Not (t) Loop Until (pky > pk_max) End Sub |
sylvi91 post贸w: 23 |  2018-05-11 12:18:07 2018-05-11 12:18:07*nk_1 Dzi臋ki za zainteresowanie tematem liczb. Sorry, 偶e dopiero teraz pisz臋 jednak nie by艂o powod贸w abym wcze艣niej si臋 odzywa艂. Pr贸bowa艂em uruchomi膰 podane makro, ale program zg艂asza艂 w trakcie uruchaminia makra b艂膮d o niezgodno艣ci typ贸w w dw贸ch liniach. 1. x_max = Range(\"A1\").Text (b艂膮d type mismatch) 2. pk_max = Range(\"A2\").Text Nie wprowadza艂em przy tym 偶adnych danych do arkusza. Odpali艂em tylko makro i nic nie uda艂o mi si臋 zdzia艂a膰 z podanym przyk艂adem. A by艂em ciekaw dzia艂ania instrukcji VBA. Jednocze艣nie nie mog臋 za bardzo zrozumie膰 zasady dzia艂ania tego Sita Ma艂gorzaty. W ostatniej tabelce w za艂膮czonym .pdf-ie wynik dzia艂ania programu to liczby naturalne nieparzyste. Wynik zawieraja wprawdzie liczby pierwsze i jak pokazuje tabelka s膮 one w okre艣lonych odst臋pach od siebie. To do艣膰 interesuj膮ce jak patrz臋 na tabelk臋. Ale ca艂y opis dzia艂ania sita niewiele mi t艂umaczy. Dokonujesz dw贸ch iteracji na dw贸ch zbiorach liczb z tego tylko rozumiem. Przez ten czas przygotowa艂em nowsz膮 wersj臋 w艂asnego programu do rozstawiania liczb pierwszych na p艂aszczy藕nie. Program dzia艂a o wiele sprawniej. Jednak to dalej bardzo surowa wersja beta. Wykorzystuje tym razem 5 tysi臋cy liczb naturalnyczh w jednym rzucie/obej艣ciu a 艂膮cznie korzysta ze 100 tysi臋cy liczb, wyznaczaj膮c liczby pierwsze. My艣l臋 偶e tym razem uda mi sie zamie艣ci膰 linki do programu bez b艂臋d贸w. Linki nie dzia艂a艂y. Nale偶y pobra膰 archiwum, rozpakowa膰 i uruchomi膰 PNP.exe. To miniaturowa aplikacja dla windows (win32) dystrybuowana bez 偶adnej licencji i gwarancji. Mirror z Google Drive. Link do programu Widok dzia艂aj膮cego programu na serwerze Interia.pl  Ponadto przygotowa艂em dwa diagramy do prezentacji liczb pierwszych . 1. Pentagon liczb pierwszych. (Liczby pierwsze wi臋ksz膮 czcionk膮). Zwi膮zek liczb pierwszych ze 艢wi臋t膮 Geometri膮. Mirror z FotoWrzut.pl  Mirror z Google Drive Pentagon Liczb Pierwszych 2. Tabela liczb pierwszych. Uporz膮dkowana tabela z pi臋cioma kolumnami i liczbami pierwszymi na czerwono. W danej kolumnie liczby pierwsze ko艅cz膮 si臋 t膮 sam膮 cyfr膮. Mirror z FotoWrzut.pl  Mirror z Google Drive Tabela Liczb Pierwszych |
tumor post贸w: 8070 |  2018-05-11 13:33:57 2018-05-11 13:33:57Bardzo du偶o miejsca po艣wi臋casz pozbawionej warto艣ci obserwacji. Je艣li szeregujesz liczby co 5, to ich ostatnie cyfry b臋d膮 zmienia膰 si臋 naprzemiennie (bo u licha ci臋偶kiego mamy system dziesi臋tny!): 2,7,12,17,22,27,32,37,.... Liczba 5 jest nieparzysta, zatem dodaj膮c kolejne pi膮tki otrzymujemy naprzemiennie liczby parzyste i nieparzyste. Parzyste (z wyj膮tkiem 2) nie mog膮 by膰 pierwsze. Dlatego wszystkie pierwsze w takim ci膮gu (poza 2) ko艅cz膮 si臋 na 7. w ci膮gu 5,10,15,20,25,... nie ma liczb pierwszych poza 5, bo dodaj膮c kolejne 5 zawsze otrzymujemy liczb臋 z艂o偶on膮 podzieln膮 przez 5 w ci膮gu 1,6,11,16,21,... oczywi艣cie wszystkie pierwsze ko艅czy膰 si臋 musz膮 na 1, bo wszystkie ko艅cz膮ce si臋 na 6 s膮 parzyste. Te obserwacje s膮 na poziomie szkolnym. Nie ma tu 偶adnego zwi膮zku z k膮tem pi臋ciok膮ta czy z艂otym podzia艂em, bo przeskakiwanie co 5 liczb nie wymaga rysowania pi臋ciok膮ta wcale, a gdy go narysujesz: nie musi on by膰 foremny. |
sylvi91 post贸w: 23 |  2018-05-11 14:25:04 2018-05-11 14:25:04*tumor Mo偶e dla Ciebie to bezwarto艣ciowe, ale ja o liczbach pierwszych niewiele by艂em w stanie sobie wyobrazi膰. Niewiele dop贸ki nie zaj膮艂em sobie przybli偶a膰 tego tematu, a偶 wreszcie siegn膮艂em po narz臋dzie programistyczne. Nigdzie wcze艣niej nie znalaz艂em takich lub podobnych nawet konstrukcji, rysunk贸w, diagram贸w, pomocy szkolnych kt贸re na poziomie podstaw贸wki b膮d藕 szko艂y 艣redniej u艂atwi艂yby zrozumienie tego szerokiego zagadnienia jakim s膮 liczby pierwsze. Czemu mimo setek tysi臋cy r贸偶nych zdj臋膰 na serwerach w internecie nie znalaz艂em takich konstrukcji/diagram贸w? Czy wed艂ug Ciebie by艂y zbyt proste do wykonania, aby by艂o warto po艣wi臋ci膰 im czas? Nie jestem matematykiem, wi臋c moja wiedza nie musia艂a by膰 wystarczaj膮ca aby rozumie膰 wcze艣niej to co sam teraz opisa艂em. W ka偶dym razie dzi臋ki za krytyczne uwagi. Mo偶e zmobilizuje mnie to w przysz艂o艣ci do wi臋kszego wysi艂ku aby zg艂臋bi膰 temat bardziej. Nie zgadzam si臋 z tob膮, 偶e liczby te nie maj膮 zwi膮zku ze 艣wi臋t膮 geometri膮, z艂otym podzia艂em i liczb膮 Phi. Ot贸偶 we藕 pod uwag臋, 偶e odst臋p pomi臋dzy kolejnymi liczbami naturalnymi na bokach danego pi臋ciok膮ta wynosi dok艂adnie 1. Gdyby liczby by艂y rozmieszczone na wierzcho艂kach by艂oby to lepiej widoczne. Przyjmijmy wi臋c to co wskazuj膮 liczby naturalne. Oleg艂o艣膰 mi臋dzy kolejnymi wierzcho艂kami pi臋ciok膮ta wynosi wi臋c powiedzmy 1 (cm/metr/km). Otrzymujemy w ten spos贸b kszta艂t foremny. Gdyby mi臋dzy kolejnymi wierzcho艂kami pi臋ciok膮ta by艂 inny odst臋p to zaznaczy艂bym to wstawiaj膮c inne liczby na wierzcho艂akch... by膰 mo偶e r贸wnie偶 niewymierne. Lub w tym przypadku tego rysunku tak jakby sumuj膮c wymiary kolejnych odcink贸w/bok贸w. Pozdrawiam. |
nk_1 post贸w: 14 |  2018-05-11 14:55:50 2018-05-11 14:55:50Na pocz膮tku o b艂臋dach w makrze: 1. x_max = Range(\"A1\").Text (b艂膮d type mismatch) W kom贸rce A1 aktywnego arkusza wpisa膰 warto艣膰 1040001 2. pk_max = Range(\"A2\").Text W kom贸rce A2 wpisa膰 wado艣膰 np. 25 Dane w kom贸rkach A1 iA2 s膮 danymi wej艣ci贸wymi dla wy偶szej przedstawionego makra w Excelu. |
sylvi91 post贸w: 23 |  2018-05-11 15:45:11 2018-05-11 15:45:11*nk_1 Pewnie zakrad艂 si臋 jeszcze jaki艣 b艂膮d w tym kodzie, bo po wpisaniu w kom贸rkach A1 i A2 odpowiednio warto艣ci odpowiadaj膮cej za ilo艣膰 wype艂nianych kolumn i wierszy, arkusz wype艂nia si臋 samymi jedynkami. Niestety na skryptach VBA si臋 nie znam i nie potrafi臋 znale艣膰 b艂臋du samodzielnie. Sprawd藕 prosz臋, czy nie ma wi臋cej b艂臋d贸w w tym makro. Jestem ciekaw efektu dzia艂ania programu. |
nk_1 post贸w: 14 |  2018-05-11 17:06:07 2018-05-11 17:06:07Nr wiersza Excela nale偶y jeszcze przeliczy膰 nast臋puj膮co: Nr nieparzysty razy 3 i dodajemy 2 Nr parzyste razy 3 i dodajemy 1 Jedynka oznacza liczb臋 z艂o偶on膮 a pusta liczb臋 pierwsz膮. W drugiej kolumnie nr wierszy+A1 (kontynuacja liczenia z kolumny pierwszej) - \"zawijanie\" wprowadzone bo sko艅czona ilo艣膰 wierszy w Excelu. |
nk_1 post贸w: 14 |  2018-05-11 17:29:53 2018-05-11 17:29:53Nale偶y pami臋ta膰, 偶e do wyznaczonego powy偶ej zbioru liczb pierwszych dodajemy jeszcze liczby 2 i 3. Dodatkowo je偶eli przyjmiemy, 偶e nr wierszy Excelu to ci膮g bit贸w dla kt贸rego jeste艣my okre艣li膰 pozycj臋 w ci膮gu oraz, 偶e bit przyjmuje warto艣膰 1 lub 0 - to mo偶emy mie膰 du偶e zbiory liczb pierwszych do analizy. |
nk_1 post贸w: 14 |  2018-05-11 17:59:57 2018-05-11 17:59:57Poni偶ej zamieszczam og贸lny schemat blokowy sita Ma艂gorzaty, kt贸ry obrazuje dzia艂anie tego sita: 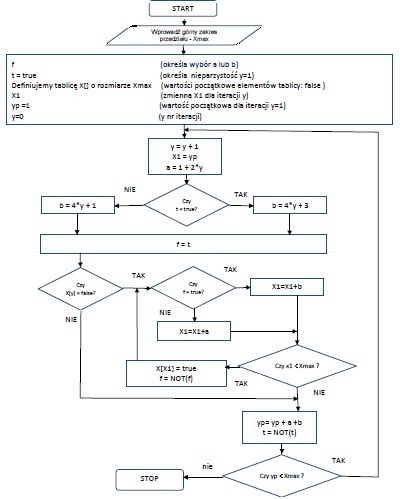 |
| strony: 1 2 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj