Statystyka, zadanie nr 4082
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
rutek2121 post贸w: 8 |  2016-01-10 16:26:05Pom贸g艂by mi kto艣 z zad. 8 na dole ost. strony? http://theta.edu.pl/wp-content/uploads/2011/02/cwiczenia-nr-6.pdf |
janusz78 post贸w: 820 | 2016-01-10 17:07:35 $ n_{0}= \left [\left(\frac{\sigma \cdot u_{1-\alpha/2}}{l}\right)^2\right ] +1.$ Obliczenia w programie R Dane > sigma=0.1 > 2l = 0.08, l =0.04 > $ 1-\alpha =0.95$ Kwantyl rz臋du $1-\frac{\alpha}{2}= 0.9975$ standaryzowanego rozk艂adu normalnego > ualpha= qnorm(0.9975) > ualpha [1] 2.807034 Niezb臋dna ilo艣膰 pomiar贸w > n0= ((sigma*ualpha)/l)^2+1 > n0 [1] 50.2465 > n0 = 51 Odpowied藕: trzeba wykona膰 co najmniej 51 pomiar贸w. Wiadomo艣膰 by艂a modyfikowana 2016-01-10 17:23:31 przez janusz78 |
rutek2121 post贸w: 8 | 2016-01-10 17:15:13 A m贸g艂bym prosi膰 o wyt艂umaczenie poszczeg贸lnych krok贸w? Okomentowanie komend? :) |
janusz78 post贸w: 820 | 2016-01-10 17:27:41 Nie ma co okomentowywa膰! Podstawiamy dane do wzoru na $ n_{0}$ Kwantyl rz臋du 0,9975 odczytujemy z tablicy standaryzowanego rozk艂adu normalnego lub za pomoc膮 programu komputerowego np R. |
rutek2121 post贸w: 8 | 2016-01-10 17:41:08 A co to qnorm()? |
janusz78 post贸w: 820 | 2016-01-10 18:17:00 To jest skr贸t od s艂贸w \" quantile normal \" - czyli komenda w programie R do wyznaczenia kwantyla rozk艂adu normalnego. Wiadomo艣膰 by艂a modyfikowana 2016-01-10 18:17:26 przez janusz78 |
rutek2121 post贸w: 8 | 2016-01-10 18:19:28 Ok, a czym jest parametr $\alpha$? Wiadomo艣膰 by艂a modyfikowana 2016-01-10 18:41:34 przez rutek2121 |
janusz78 post贸w: 820 | 2016-01-10 18:47:15 $ \alpha $ to wsp贸艂czynnik istotno艣ci. Wyznacza si臋 go na podstawie poziomu istotno艣ci $ 1- \alpha.$, kt贸ry w tym przypadku wynosi $ 95\% = 0,95.$ |
rutek2121 post贸w: 8 | 2016-01-10 18:58:41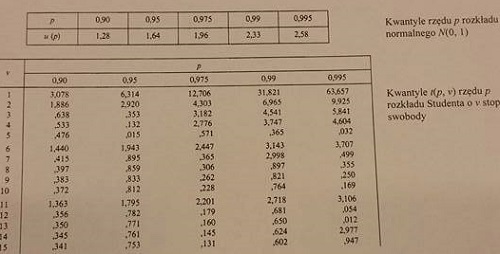 A sk膮d mam wzi膮膰 warto艣膰 kwantyla rozk艂adu normalnego je艣li do dyspozycji mam jedynie dwie takie tabele? |
janusz78 post贸w: 820 | 2016-01-10 19:38:45 W tym przypadku podstawiamy z g贸rnej tabeli warto艣膰 mniej dok艂adn膮 kwantyla $ p = 2,33 $ dla $ 1- \frac{\alpha}{2}= 0,99.$ |
| strony: 1 2 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj