Kąt między dwiema prostymi

Kątem między prostymi nazywamy mniejszy z wyznaczonych przez nie kątów. Jest on nie większy od kąta prostego.

Niech będą dane dwie proste k: y = m₁x + k₁, i l: y = m₂x + k₂

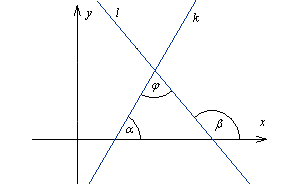
Z rysunku otrzymujemy α + φ = β stąd φ = β - α
tgφ = $tg (β - α) = \frac{tg β - tg α}{1 + tg α tg β} = \frac{m_{2} - m_{1}}{1 + m_{1} m_{2}}$

Warunkiem koniecznym i wystarczającym na to, by proste były równoległe, jest, by tgφ = 0, tzn. m1 = m2.
Warunkiem koniecznym i wystarczającym na to, by proste były prostopadłe, jest, by tgφ był nieokreślony, tzn. 1 + m1m2 = 0.

Kąt między prostymi k i l zadanymi równaniami odpowiednio:
k: A₁x + B₁y + C₁ = 0,
l: A₂x + B₂y + C₂ = 0,
gdzie A₁² + A₁² > 0 i A₂² + A₂² > 0, daje się wyznaczyć ze wzorów:

tgφ = $\frac{A_{1} B_{2} - A_{2} B_{1}}{A_{1} A_{2} + B_{1} B_{2}}$

cosφ = $\frac{A_{1} A_{2} + B_{1} B_{2}}{\sqrt{A_{1}^{2} + B_{1}^{2}} \sqrt{A_{2}^{2} + B_{2}^{2}}}$

sinφ = $\frac{A_{1} B_{2} - A_{2} B_{1}}{\sqrt{A_{1}^{2} + B_{1}^{2}} \sqrt{A_{2}^{2} + B_{2}^{2}}}$