logowanie

Równanie parametryczne i kanoniczne prostej

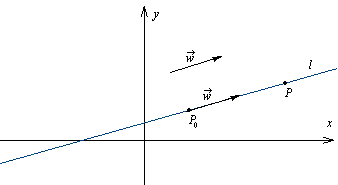
Rozważmy prostą l, która przechodzi przez punkt P₀(x₀, y₀) i jest równoległa do wektora ${\displaystyle \overrightarrow{w}}=$. Przenieśmy wektor ${\displaystyle \overrightarrow{w}}$ w taki sposób, aby jego początek znalazł się w punkcie P₀, wtedy wektor ten będzie leżał na prostej l. Punkt P(x, y) leży na prostej l wtedy i tylko wtedy, gdy wektor ${\displaystyle \overrightarrow{P_{0}P}}=$ jest iloczynem wektora ${\displaystyle \overrightarrow{w}}$ przez pewną liczbę t, tzn. jeżeli

$\left\{\begin{array}{c}x-x_0=mt\\ y-y_0=nt\end{array}\right.$
lub
$\left\{\begin{array}{c}x=x_0+mt\\ y=y_0+nt\end{array}\right.$

Równania te nazywamy równaniami parametrycznymi poszukiwanej prostej l, gdzie zmienny parametr t należy do zbioru liczb rzeczywistych.

W równaniach tych wynika, że t = 0 odpowiada na prostej l punkt P₀(x₀, y₀), czyli początek wektora ${\displaystyle \overrightarrow{w}}$, a wartości t = 1 odpowiada koniec wektora ${\displaystyle \overrightarrow{w}}$.
W ten sposób równania parametryczne ustalają na prostej l skalę równomierną dla zmiennego parametru t.

W przypadku, gdy wektor ${\displaystyle \overrightarrow{w}}$ jest wektorem jednostkowym w równaniach parametrycznych prostej, parametr t oznacza odległość punktu P(x, y) ze znakiem + lub - prostej od punktu stałego.

Równanie kanoniczne prostej

Warunek równoległości wektorów ${\displaystyle \overrightarrow{P{P}_0}}$ i ${\displaystyle \overrightarrow{w}}$ można zapisać we współrzędnych:
$\frac{x-x_0}{m}=\frac{y-y_0}{n}$

Jest to równanie kanoniczne prostej l.

© 2024 math.edu.pl      kontakt